서론
수학교육에서 수학사 활용에 대한 논의는 오래전부터 제기되어 왔으며, 대표적으로 De Morgan, Poincaré, Klein, Lakatos에 의해 옹호되어왔다 (Tzanakis et al., 2000). 수학사가 수학 학습을 돕는다는 주장은 수학 내용뿐 아니라 형식, 표기, 용어, 계산법, 표상양식 등이 진화하는 모습이 수학사에 나타난다는 점을 근거로 하고 있다. Woo (2018)는 과거 역사 속에서 다루어졌던 수학 언어적, 형식적 접근뿐 아니라 직관적, 시각적, 비형식적인 접근이 갖는 의미를 재평가하는 활동이 오늘날의 수학 형식에 대해서 새로운 시각을 제공함으로써 장단점을 인식하고 심화된 이해를 도울 수 있다고 말한다. 이는 수학사 활용 목적을 인지적 측면에 두는 것으로, 역사 속에서 사장된 옛 지식의 출현이 학교수학의 개념과 법칙들을 재검토하는 계기를 제공함으로써 그동안 당연시하여 의문조차 갖지 않았던 수학적 아이디어를 재음미하게하여 보다 의미있는 사고활동을 유도한다 (Arcavi, 1991; Woo, 1998)는 주장과 상통한다.
본 연구는 역사 속에서 다루어진 수학의 형식적, 비형식적 접근이 갖는 의미를 재평가하는 작업의 일환으로, 우리나라 고유의 전통수학인 조선산학에 초점을 맞추고자 한다. 조선산학 관련 연구는 2000년대에 들어서서 수학 및 수학교육 학문공동체에서 활성화되기 시작하여 지난 이십여년동안 지속적으로 이루어져 왔다. 2002년 기초학문육성사업의 국학고전연구 분야에서 ‘조선시대의 산학서 번역’ 과제가 수행되어 그 결과물로 국역 산학서가 널리 보급된 것이 연구자 집단을 확대하고 연구 주제를 심화시킬 수 있었던 토대가 되었다고 본다. 비록 양적으로 풍부하다고 할 수 없지만, 그동안 조선산학서가 다루고 있는 수학 개념과 원리, 계산법 등을 수학적 차원에서 분석하는 연구 (Her, 2005; Hong, Hong & Lee, 2012; Kim, 2019; Kim & Yun, 2009)와 조선산학을 교육적으로 활용하는 방안을 탐색하는 연구 (Choi, 2017; Kim, Kim & Lee, 2017; Yang, 2018)가 수행되었다. 수학교육에서의 활용을 논한 연구 중에서 Kim, Kim과 Lee (2017)는 조선산학서의 망해도술(望海島術) 단원을 중학교 2학년 닮음 단원에서 활용한 교수학습자료로 제시하였으며, Yang (2018)은 망해도술을 삼각형의 닮음비를 이용하여 학생들이 직접 거리와 높이를 측정하고 해결하는 수행평가 활동으로 재구성하였다. 또한 Choi (2017)는 원주율과 관련된 조선산학서의 내용을 분석하여 원주율에 대한 심화학습을 위한 교수·학습활동자료로 조직화하였다.
한편 사회적 배경과 문화적 관점을 병행하여 수학의 역사를 살펴볼 것을 주장한 연구가 있다. Gulikers와 Blom (2001)이 강조한 문화적 관점은 수학이 오랜 시간에 걸쳐 점진적으로 발달되어 온 과정에서 사회적, 문화적 요인이 작용했음을 이해하는 것이다. 현재 수학이 고대 그리스 수학의 전통과 근대 유럽 수학에 근간을 두고 있는 서양수학의 산물이기도 하지만, 다양한 문화권의 수학적 아이디어와 연구 노력이 융합되어 역동적으로 발달해온 지식체계임 (Ascher, 1991; D'Ambrosio, 1985)을 이해하는 것도 대표적 사례이다. 수학사의 문화적 관점에서 보면, 조선산학 또한 우리나라 고유의 전통수학을 토대로 중국을 비롯한 다른 문화권의 수학지식을 수용하고 발전시키는 과정을 거쳐온 지적 유산이라고 할 수 있다. 특히, 조선산학의 역사에서 18세기는 특별한 의미를 가지는데, <산학계몽> 등의 산학서를 경전시했던 조선 전기의 학문적 경향에서 탈피하여 <기하원본>과 <수리정온> 등의 한역서(漢譯書)를 통해 서양수학을 부분적으로 수용한 시기이기 때문이다. 이 시기의 서양수학에 대한 조선지식인들의 반응을 분석한 Koo (2010)는 서명응, 황윤석, 홍대용 등의 다수의 유학자들이 서양수학을 탐구한 학자군이었음을 밝히고 있다. Choi (2020)는 분석 대상을 18세기로 특정하여, 이 시기에 저술된 서명응의 <고사십이집>, 황윤석의 <산학입문>, 홍대용의 <주해수용>을 포함한 총 7권의 조선산학서의 대수 영역에서 서양수학의 표현과 계산법이 반영된 내용을 제시하였으며, 전통적 계산법과 서양식 계산법이 공존한 사례와 대체된 사례를 살펴본 바 있다. 일부 산학서에서 기존의 산대 조작 계산법 대신 필산을 제시하고 있는 사례, 사율법을 사용한 비례식의 형식화 사례, 연립일차방정식 계산법이 점진적으로 형식화되어가는 사례, 제곱근 계산의 필산 사례가 중점적으로 제시되었다. 그런데 지금까지 수행된 조선산학 연구 중에서 18세기 후반의 조선산학에 대해 기하 영역을 중심으로 체계적으로 살펴본 연구는 찾아보기 힘들다. 앞에서 기술한 인지적 측면과 문화적 측면에서의 수학사 활용가능성을 감안할 때 상당히 아쉬운 부분이라고 할 수 있다.
본 연구는 중국한역서를 통해 서양수학이 본격적으로 수용되었던 18세기 후반의 사회문화적 배경하에 저술된 조선산학서에서 기하 영역, 특히 평면도형과 관련된 내용에 주목한다. 본 연구의 목적은 18세기 후반 조선산학서에 나타난 기하 영역의 평면도형 관련 내용들이 이전 시기와 비교하여 어떻게 차별화되어 다루어지고 있는지를 분석하는 것이다. 평면도형과 관련된 설명과 계산법이 어떻게 변화되었는지와 그 과정에서 드러나는 수학적 사고의 특징이 무엇인지를 살펴볼 것이다. 이를 위해 본 연구에서는 18세기 후반에 저술된 서명응의 <고사십이집>과 황윤석의 <산학입문>, 홍대용의 <주해수용>을 주 분석문헌으로 선정하여 이전 시기의 조선산학서와 비교할 것이다. 조선산학서에 나타난 여러 계산법과 수학적 사고의 변화 과정을 고찰하는 것은 우리나라 고유의 전통수학에서 오늘날 학교수학으로 이어지는 연속적인 흐름 속에서 기하 영역을 이해하는 것에 도움이 될 것으로 본다.
조선산학의 역사에서 18세기의 의미
수학사와 사상사 측면을 포괄하여 조선산학에 대한 문화사적 분석을 시도한 Kawahara (2017)에 따르면, 조선산학은 양란(兩亂)을 기점으로 성격을 달리한다. 조선 전기에 해당하는 16세기까지의 조선산학은 중국산학서 <산학계몽>, <양휘산법>. <상명산법>을 경전시하여 철저하게 중국산학 중심의 학문적 경향을 띠었던 시기이다. <산학계몽>과 <양휘산법>은 계산 도구인 산대, 즉 주(籌)에 기반한 주산서라고 할 수 있는데, 대표적으로 주(籌)를 이용한 다항식과 방정식의 표기법이자 다항식의 간단한 계산법인 천원술을 다루고 있다. Kim과 Kim (2009)과 Kawahara (2017)는 조선산학의 첫 번째 전성기를 산학제도가 정비되고 국가 차원의 적극적인 산학진흥책으로 인해 산학연구가 활발했던 세종부터 성종에 이르는 시기라고 말한다. 그러나, 아쉽게도 16세기까지 독자적으로 저술된 조선산학서를 찾아볼 수 없으며, 이 시기는 산학의 경전에 해당하는 중국산학서를 이해하고 해석하는 단계에 머무른 것으로 보인다. 한 가지 주목할 것은 동시대 중국인 명(明)의 산학이 계산 도구를 산대에서 주판으로 교체한 주산(珠算) 기반의 실용 수학이었지만, 조선산학은 여전히 산대 기반의 주산(籌算)을 중심으로 함으로써 주산(珠算)의 흔적조차 찾아보기 힘들다는 점이다.
Kawahara (2017)는 양란(兩亂)이 끝난 17세기 중엽 이후를 비로소 중국산학 의존에서 탈피하기 시작하여 독자적 발전을 이루었던 시기로 보고 있으며, 이 시기의 조선산학을 동국산학, 동산(東算)이라고 부른다. 17세기 중엽 경선징의 <묵사집산법>과 박율의 <산학원본>의 출간을 시작으로, 18세기에는 최석정의 <구수략>을 비롯한 다수의 조선산학서가 저술되었다는 점에서 조선산학의 제2의 전성기라고 할 수 있다. Kawahara (2017)은 조선 고유의 산학인 동산(東算)이 17세기 중엽의 경선징으로부터 태동되어 18세기 전반 홍정하의 <구일집>에 이르러 성립되었다고 보고 있다. 이미 중국산학에서는 그 전통을 잃어버린 산대 기반의 계산술과 천원술을 보전하여 고차방정식 해법인 증승개방법으로 한 단계 발전시킨 <구일집>이야말로 조선산학의 독자적 발달인 동산 성립의 지표이다. 이러한 사회문화적 배경 속에서 17세기와 18세기에 걸쳐 다수의 산대 기반 주산서가 저술되었는데, <묵사집산법>, <산학원본>, <구수략>, <주서관견>, <구일집>, <산학입문>, <주해수용> 등이 해당된다.
이 중에서 18세기 후반에 황윤석(1729~1791)이 저술한 <산학입문>은 각종 산법에 대해서 <산학계몽>, <양휘산법> 등을 인용하고 자신의 수학적 식견을 가미하여 문제의 해법을 제시하고 있는 책으로, 부분적으로 일반화된 이론적 설명을 시도하고 있는 것이 특징이다. 거의 같은 시기에 홍대용(1731~1783)이 저술한 <담헌서> 외집 4, 5, 6권에 해당하는 <주해수용>은 구체적인 수치를 갖는 문제를 전형적인 사례로 하여 각 산법의 알고리즘을 설명하는 전통적인 산학서 기술 방식을 따르고 있다. 그런데 선행연구에서 주목한 <주해수용>이 가지는 의의는 서양의 비례식인 사율법을 설명하고 삼각함수에 해당하는 삼각팔선을 도입하는 등 서양수학 내용을 담고 있다는 점이다 (Hong, 2019; Lee, 2007). 아마도 저자 홍대용의 중국 사신 파견 경험과 북경에서의 예수회 선교사와의 교류 경험이 서양수학 수용에 계기가 되었을 것이라는 것이 자연스러운 추측이다.
조선산학 관련 선행연구들은 조선산학의 역사에서 18세기가 가지는 특별한 의미를 공통적으로 언급한다 (Choi, 2020; Kawahara, 2017; Koo, 2010). 바로 18세기가 서양수학을 한역(漢譯)한 중국산학서가 유입되고 본격적으로 서산(西算)을 연구하고 부분적으로 수용하던 시기였기 때문이다. 일찍이 중국은 명(明)말 Matteo Ricci의 입국을 시작으로 예수회 선교사들이 서양수학을 비롯한 서양과학 지식을 소개하였으며, 명(明)말과 청(淸)초의 중국은 정밀한 역법 개정을 목적으로 삼각법을 비롯한 서양수학 지식을 적극적으로 수용하는 모습을 보였다. Needham (2000)은 이로 인해 중국 고유의 산학 시대가 종말을 고했다고 평가하지만, 중국산학이 서양수학인 서산(西算)을 수용한 필산(筆山)의 형태로 청(淸) 중엽까지는 독자적 발전을 이루었다고 보는 주장도 있다 (Kawahara, 2017). 반면에 조선은 서양선교사들이 서양수학을 직접 전래한 것이 아니라, 중국을 왕래한 조선 관료들이 예수회 선교사와 교류하거나 중국을 통해 유입한 서양수학의 한역본 또는 서양수학을 반영한 중국산학서를 개인적 수준에서 탐구하는 방식으로 이루어졌다. 앞에서 살펴본 홍대용이나 <고사십이집>의 저자 서명응은 연행사로서 중국에 다녀왔다는 공통점이 있다. 서명응의 <고사신서> 산수요략은 인도의 포지금과 네이피어 계산 막대를 변형한 주(籌)를 이용한 책산(策算)의 해법을 제시하고 있으며, <고사십이집> 수예는 오늘날의 사칙계산 알고리즘과 동일한 유럽 산술을 인도아라비아 숫자 대신에 한자수사로 표기한 필산(筆算)을 소개하고 그 편리함을 강조한다.
한편 18세기를 즈음하여 조선사회로 유입된 서양수학의 한역본은 <천학초함>, <기하원본>, <수리정온> 등이 대표적이다. <천학초함>은 18세기 초 최석정의 <구수략> 인용목록에 나타나며, 1629년 李之藻가 명(明)말 예수회 선교사들이 전한 서학서를 한역한 책들을 모은 학술총서인데, 여기에는 Euclid <원론>의 한역본인 <기하원본>과 서양산술서의 한역본인 <동문산지>가 포함되어 있다 (Kim & Kim, 2009). <기하원본>은 Clavius의 <유클리드원론주해> 15권 중에서 전반부 6권을 Matteo Ricci가 구술하고 徐光啓가 필록한 것이고, <동문산지>는 Matteo Ricci가 구술하고 李之藻가 필록한 Clavius의 <실용산술개론>에 중국산법을 덧붙인 책이다 (Kawahara, 2017). <수리정온>은 康熙帝의 명으로 중국과 서양의 천문학, 음악, 수학 등 과학지식을 집대성하여 간행한 <율력역원> 100권 중 53권에 해당하는 책이다. 방정, 개방 등 중국 전통적인 계산법뿐 아니라 대수, 삼각함수, 차근방비례 등 서양 산법을 통합하여 다루고 있다는 것이 특징이다. 18세기 후반의 서양수학에 대한 조선지식인들의 반응을 분석한 Koo (2010)는 대표적인 서산(西算)으로 <기하원본>과 <수리정온>을 들고 있으며, 당시 조선지식인들에게 역대 제일 위대한 수학서로 평가받은 저작이었다고 설명한다. 특히, <수리정온>은 황윤석이 <산학입문>과 서명응의 <고사십이집>과 <고사신서>에서도 많은 내용을 인용하고 있는 서양수학을 담은 한역서이다.
이와 같이 조선산학의 역사에서 18세기는 <산학계몽> 등의 중국산학서를 경전시했던 조선 전기의 학문적 경향에서 탈피하여 <기하원본>과 <수리정온> 등의 한역서를 통해 서양수학을 부분적으로 수용한 시기라고 할 수 있다. 수학사의 문화적 관점에서 보면, 18세기는 중국을 매개로 서양 문화와의 상호작용 속에서 조선산학이 성장하고 발전해간 시기이다. 그런데 조선 전기에 동시대 중국의 실용적인 주판 기반의 주산(珠算)이 산대 기반의 주산(籌算)을 대체하지 못한 것처럼, 18세기 또한 서산(西算)이 기존의 전통산학인 주산을 대체하는 수준에는 이르지 못했다는 것이 일반적 평가이다. 특히, 서양수학이 본격적으로 수용되었던 18세기 후반은 산대 조작을 기반으로 하는 주산이 여전히 조선산학의 중심인 상황에서, 일부 유학지식인들이 서산(西算)과 필산(筆算)을 연구하여 보급하고자 노력했던 시기로, 전통수학의 산대셈과 서양수학 영향의 필산이 공존하였던 시기라고 할 수 있다.
연구방법
본 연구는 서양수학이 중국을 통해 조선에 본격적으로 유입되어 영향을 미친 시기인 18세기 후반의 조선산학에 주목한다. 18세기 후반 조선산학의 기하 영역에서 이전 시기와 비교하여 변화된 내용과 특징을 살펴보기 위해서, 18세기 후반에 저술된 서명응의 <고사십이집>과 황윤석의 <산학입문>, 홍대용의 <주해수용>을 분석의 주 문헌으로 선정하였다. <고사십이집>과 <주해수용>은 선행연구에서 서양수학의 계산법이 일부 수록된 것으로 확인된 문헌이며 (Choi, 2013), <산학입문>은 도형에 대한 개념적 접근으로의 변화가 언급된 바 있다 (Chang, 2009; Choi, 2013). 또한 비교 문헌으로 경선징의 <묵사집산법>과 홍정하의 <구일집>을 선정하였다. <묵사집산법>과 <구일집>은 다수의 선행연구에서 각각 17세기 후반과 18세기 전반을 대표하는 조선산학서로 언급되고 있을 뿐만 아니라 기하 영역에 해당하는 단원을 전통적인 계산법으로 구성하고 있기 때문에 비교 분석에 적합하다고 판단하였다. 문헌 연구에서 1차 사료는 생생한 원자료를 통해서 오늘날 수학에서 익숙하지 않은 수학적 사고와 의사소통 방법에 대한 이해를 증진시킨다 (Bruckheimer & Arcavi, 2000)는 장점이 있으므로, 1차 사료와 이를 번역한 2차 자료 모두를 분석 대상으로 하였다.
분석 대상 조선산학서에서 기하 영역에 해당하는 단원을 선정하는 과정은 조선산학서들이 대체적으로 동양 산학서의 원형인 <구장산술>의 구장(九章)에 대응하는 유사한 단원이나 이를 좀 더 세분화한 단원 체계를 가지고 있다는 점을 활용하였다. 구장명수(九章名數)로 시작하고 있는 <산학입문>의 설명에 의하면, 구장 중에서 방전과 구고, 소광, 상공이 기하 영역과 관련이 깊다. 방전(方田)은 여러 가지 모양의 땅의 넓이를 구하는 장이며, 구고(句股)는 직각삼각형의 성질을 활용하여 높이나 길이, 폭이나 거리를 구하는 장이다. 소광(少廣)은 넓이를 가지고 사각형의 한 변의 길이나 원의 지름을 제곱근을 이용하여 구하는 장이고, 상공(商工)은 토목공사의 공정과 부피를 다룬다. 본 연구에서는 제곱근 계산과 입체도형 부분은 제외하고 순수하게 평면도형과 관련된 단원으로 분석 대상을 한정하였으며, Table 1은 선정한 각 산학서에서 평면도형의 성질과 측정을 다루고 있는 방전과 구고과 관련된 단원을 보여주고 있다.
조선산학서의 해당 단원을 수학적 표현과 계산법을 기준으로 일차적으로 살펴본 결과, 평면도형의 넓이 계산법과 설명방식, 근삿값의 표현, 도형 그림의 등장 등 이전 시기와 달라진 변화가 확인되었다. 본 연구에서는 해당 항목의 변화된 내용을 중심으로 다음과 같은 분석의 초점을 설정하였다. 첫째, 평면도형 관련 문제해결과정에서 이전 시기와 비교하여 변화가 보이는 설명과 계산법은 무엇인가? 둘째, 평면도형 관련 문제해결과정에서 수학적 논리의 엄밀성은 어떻게 나타나는가? 셋째, 18세기 후반 산학서에 새롭게 등장한 평면도형 관련 주제는 무엇이고, 그 특징은 어떠한가?
결과 분석 및 논의
18세기 후반은 산대 조작의 주산(籌算)이 여전히 조선산학의 중심인 가운데, 일부 산학서를 통해 붓으로 기록하여 계산하는 서양의 필산(筆算)이 소개되던 시기이다 (Choi, 2020; Kawahara, 2017). 본 연구가 살펴본 <산학입문>과 <주해수용>은 기본적으로 산대 계산을 전제로 쓰여진 산학서인 것에 반해, <고사십이집>은 필산을 기반으로 집필된 산학서라는 차이가 있다. 일단 이전 시기와 달라진 계산 도구나 기록 방식의 변화는 <고사십이집>에서만 찾아볼 수 있지만, 본 연구의 분석과 논의의 초점은 평면도형 관련 문제해결에서 사용된 계산법과 설명방식에 두었기 때문에 산대 계산과 필산 여부는 논외로 하였다. 또한 세 권의 산학서에서 계산법과 수학적 표현, 다루는 주제의 변화가 공통적으로 나타난 경우도 있었지만, 분석 항목에 따라서는 일부 산학서에서만 변화 사례가 관찰되고 있었음을 밝힌다. 18세기 후반 산학서에 나타난 평면도형 관련 내용의 변화를 세 가지 초점에 맞추어 분석한 결과는 다음과 같다.
도형 자체에 대한 인식과 해법의 다양화
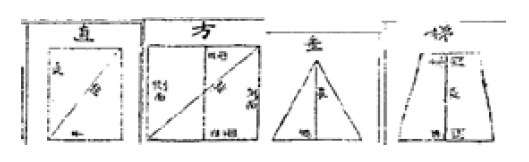
18세기 후반 산학서들이 다룬 기하 영역의 평면도형 관련 일부 맥락에서 제시된 설명과 사용된 계산법에서 이전 시기와 다른 변화 사례가 확인된다. 첫 번째 변화는 도형을 측정의 대상으로만 다루었던 기존의 접근방식에서 벗어나 도형의 구성요소와 성질에 주목하는 방식으로의 전환, 즉 탐구의 대상으로서 도형을 인식하기 시작한 점이다. 이러한 판단이 가능한 근거로 다음과 같은 사례를 들 수 있다. <묵사집산법>과 <구일집>의 ‘전무형단문’에서 다루어지는 평면도형은 방전(方田), 직전(直田), 원전(圓田) 등 땅의 넓이를 구하는 맥락에서 길이(長)와 너비(闊, 平)와 같은 구성요소에 대한 별도 설명 없이 계산법만이 제시된다. 이에 대해 Choi (2013)는 조선산학의 도형이 오랜 시간동안 그 자체로서 탐구대상이 되지 못한 채 실생활상황과 연계된 측정대상이었다고 설명한 바 있다. 반면에 <산학입문>의 ‘방전구적법’에서 제시되는 도형의 이름과 그림은 넓이 측정에서 기하 도형으로의 전이를 찾아볼 수 있는 사례이다 (Chang, 2009). Figure 1은 <산학입문>에 도형 설명과 함께 제시된 그림이며, 전(田)이 생략된 직(直, 직사각형), 방(方, 정사각형), 규(圭, 이등변삼각형), 제(梯, 사다리꼴)의 이름으로 길이와 너비, 높이와 밑변 등의 도형의 구성요소를 보여주고 있다.
더불어 정사각형 ‘방(方)’을 직사각형 ‘직(直)’의 구성요소를 사용하여 ‘장과 평이 같다’로 설명한다거나, 마름모 ‘사(梭)’를 이등변삼각형 ‘규(圭)’를 사용하여 ‘두 개의 규가 밑변이 서로 맞닿은 것이다’로 설명하는 방식은 도형들을 성질이나 구성요소에 기반하여 관계 속에서 파악하고자 하는 사례라고 해석할 수 있다. 특히, ‘규(圭)’에 대한 추가 설명에서, ‘삼각부터 시작하여 사각, 오각 이상의 모든 각의 크기가 같은 여러 다각형(凡角形), 즉 정다각형의 경우에 그 넓이를 이등변삼각형으로 분할하여 구한다’는 일반화된 설명은 도형을 탐구 대상으로 접근한 사례로 해석할 수 있다.
실생활 맥락의 도형의 측정에서 도형 그 자체의 탐구로 변화해가는 과도기적 모습은 <주해수용>의 내편 上의 양전법(量田法)과 면적법(面積法)에서 보다 확연히 드러난다. 양전법이 기존 산학서와 마찬가지로 방전, 직전, 구고전, 규전, 제전의 땅의 넓이를 구하는 단원이라면, 면적법은 다른 산학서에서는 찾아볼 수 없는 단원 명칭으로’평면의 넓이를 구하는 것(面積者 平面之積)‘으로 설명되고 있다. 제시되는 도형 이름은 정방면(正方面, 정사각형), 장방면(長方面, 직사각형), 원면(圓面, 원), 호시면(弧矢面, 활꼴), 삼각면(三角面, 정삼각형)이다. 도형 이름들이 오늘날과 약간의 차이가 있긴 하지만, 기존에 사용했던 실생활 맥락인 ‘전(田)’을 대신하여 평면을 의미하는 ‘면(面)’을 사용한 것은 땅이라는 사물의 모양이 평면도형으로 개념화되는 과도기적 상태에 있다는 점에서 의미가 있다. 한 가지 주목할 것은 여러 가지 넓이를 갖는 평면도형을 한자 모양과 대응시켜 설명하고 있다는 점이다. 예를 들어, ‘길이가 1척이고 너비가 1척이면 넓이 1척이 되는데 이것은 한자 口(구)와 모양이 같다(長一尺廣一尺謂之積一尺 如口字是也)’, ‘길이 2척, 너비 2척은 田(전)과 모양이 같다(長二尺廣二尺謂之積四尺 如田字是也)’, ‘길이 3척, 너비 3척은 井(정)과 모양이 같다(長三尺廣三尺謂之積九尺 如井字是也)’ 등의 설명이 해당된다. 이 단원은 단위 넓이에 대한 설명이 제시되고 있다는 점과 도형의 형태 맥락이 전통적인 땅의 모양으로부터 보다 상징적인 한자(漢字) 모양으로 변화하였다는 점에서도 의미를 찾아볼 수 있다. 반면에 길이 단위인 ‘척’과 넓이 단위인 ‘척2’을 구분하지 않고 여전히 ‘척’만을 사용하고 있다는 점은 한계이다.
두 번째 변화는 서양수학의 계산법인 서법(西法)을 별해로 추가 제시한 사례들이 관찰된다는 점이다. 그 대표적 사례로 직각삼각형의 넓이 계산법을 들 수 있다. <묵사집산법>을 비롯한 기존 산학서에서 구고의 넓이는 구(짧은 변, 밑변)와 고(긴 변, 높이)를 서로 곱하여 2로 나누어 구한다. 반면에 <고사십이집> 구고의 넓이는 세 가지로 다양화되어 제시된다. 첫째는 구와 고의 곱을 반으로 나누는 전통적인 방법이고, 두 번째는 현(빗변)과 중수선(中垂線, 직각인 꼭짓점에서 현에 내린 수선)을 곱하여 2로 나누는 방법, 세 번째는 일명 헤론의 공식이다. 두 번째 방법의 중수선은 기존의 조선산학서에서 찾아볼 수 없는 용어로, 그동안 수선이나 높이 개념에 주목하지 않았던 조선산학서가 <수리정온>의 영향을 받아 새로운 개념과 계산 방법을 추가로 제시한 경우라고 볼 수 있다. 세 번째 방법은 구고현 세 변의 길이의 합의 반을 반총(半總)이라 하고, 반총에서 세 변을 뺀 길이를 삼교(三較)라고 한 후, 삼교를 모두 곱한 후 다시 반총을 곱한 값의 제곱근으로 직각삼각형의 넓이를 설명한다. 이를 수식으로 나타내면, 세 변의 길이를 각각 $a, b, c$라고 했을때, 반총은 $\frac{a+b+c}{2}=s$, 삼교는 $s-a$, $s-b$, $s-c$를 의미하며 직각삼각형의 넓이는 $S=\sqrt{s(s-a)(s-b)(s-c)}$라고 표현할 수 있다. 헤론의 공식으로 잘 알려진 있는 이 계산법은 서양수학의 한역본인 <수리정온>의 면부-구고에서 인용한 내용이다 (Seo, 2017).
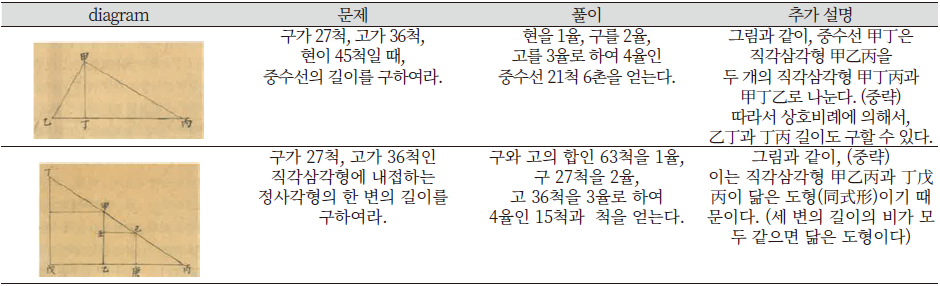
특히, 헤론의 공식의 도입은 직각삼각형에 내접하는 원의 반지름을 구하는 문제와 연결되어 관련 해법을 다양하게 제시하고 있다. <고사십이집> 구고팔선 단원의 ‘구가 27척이고 고가 36척, 현이 45척인 직각삼각형에 내접하는 원의 지름은 얼마인가?’ 문제에 대한 도해와 세 가지 풀이는 Figure 2와 같다.
Method ①은 사율비례를 이용한 것으로, 직각삼각형 甲丙乙에서 구고현을 각각 $a,b,c$라고 하면 비례식 $(a+b+c):b = a:r$로 나타낼 수 있다. 내항의 곱과 외항의 곱이 같다는 비례식의 성질을 이용하면 지름 2r이 $\frac{2\times{a}\times{b}}{a+b+c}$로 구해진다. 이 방법은 일찍이 <구장산술>의 구고장에서 사용한 방법으로, <구일집> 구고호은문에서도 이와 동일한 해법을 제시하고 있다. 다만 <구일집>은 비례식이나 다른 일체의 설명 없이 ‘구와 고의 곱의 두 배를 구, 고, 현의 합으로 나눈다’는 알고리즘만을 제시하고 있다는 점에서 차이가 있다. 반면에 방법 ②와 방법 ③은 기존의 조선산학서에서는 찾아볼 수 없는 풀이이다. Method ②가 타당한 이유는 저자 서명응이 기술한 바와 같이, 사각형 己丙戊丁이 정사각형이므로 己丙과 丙戊의 합은 내접원의 반지름의 두 배 甲己와 戊乙의 합이 현 甲乙과 같으므로 세 변의 합에서 현의 두 배를 빼면 지름을 얻을 수 있기 때문이다. 이 과정 을 확인하기 위해 甲己와 甲庚을 $d$, 乙庚과 乙戊를 $e$라 하면, $(a+b+c) - 2c = (a+b+c) - 2(d+e) = 2r$을 유도할 수 있다. Method ③은 반총과 삼교를 사용한 일명 헤론의 공식 $S=\sqrt{s(s-a)(s-b)(s-c)}$과 $S = rs$로부터 $r = \frac{S}{s} = \frac{\sqrt{s(s-a)(s-b)(s-c)}}{s} = \sqrt{\frac{(s-a)(s-b)(s-c)}{s}}$가 쉽게 유도된다.
계산법과 관련된 세 번째 변화는 서양수학의 계산법이 반영되어 기존 풀이법을 대체한 경우이다. 대표적인 것으로 Ⅱ장에서 살펴본 서양의 비례사율이 기하 영역의 문제 풀이에서 일반적인 알고리즘으로 사용되고 있는 것을 들 수 있다. 기존의 <묵사집산법>과 <구일집>이 전통적인 금유술을 사용하고 있다면, <산학입문>, <주해수용>, <고사십이집> 모두 주어진 양과 구해야 할 양을 1율에서 4율까지의 관계로 파악하는 서양의 비례사율을 적극적으로 사용하고 있다. 사율사이의 비례관계를 논하는 내용이 <산학입문>의 비례사율, <주해수용>의 사율법, <고사십이집>의 사율비례에 설명되어 있으며, 특히 <고사십이집>은 동치인 비를 표현한 비례식에서 내항의 곱과 외항의 곱이 같다는 원리를 ‘비례관계가 같으면 2율과 3율을 곱한 수가 1율과 4율을 곱한 수와 같다’고 설명하고 있다. 실제 문제풀이에서도 <주해수용> 내편 下의 비례구고 단원의 21개 문제와 중비례구고 단원의 6개 문제 모두 기존의 금유율의 표현이 아닌 새로운 비례사율의 개념으로 풀이가 제시되고 있다. 가장 간단한 예로, 평구고 단원의 ‘정구고(正句股, 세 변의 길이의 비가 3:4:5인 직각삼각형)에서 구(勾, 밑변)가 15일 때, 고와 현의 길이를 구하여라’ 문제의 풀이는 ‘고(股)를 구하려면 구 3을 1율로 하고, 고 4를 2율로 하고, 주어진 구의 길이 15척을 3율로 하여 고를 구한다. 2율과 3율을 서로 곱한 수 60척을 1율로서 나누면 4율 2척을 얻는다’로 제시되고 있다. 앞에서 살펴본 <고사십이집>의 ‘구가 27척이고 고가 척, 현이 45척인 직각삼각형에 내접하는 원의 지름은 얼마인가?’에 대한 풀이법에도 구하고자 하는 내접원의 반지름을 4율로 놓고 비례사율의 원리를 적용하여 문제를 해결한다(Figure 2 참조)
엄밀해진 수학적 논리
18세기 후반 산학서의 평면도형 관련 내용에서 수학적 논리의 엄밀성 측면에서 이전 시기와 다른 변화 사례가 확인된다. 조선산학서는 다루는 맥락이나 계산법을 기준으로 단원별로 문제들을 모아 <문제-답-풀이> 형식으로 기술한 일종의 문제해설서라고 설명된다. 문제 풀이는 각 알고리즘이 어떻게 도출되었는지와 왜 옳은지에 대한 타당화 과정이 생략된 채, 구체적인 수치가 대입된 계산 절차만을 기술하고 있으며 해법을 정당화하는 서술내용을 찾아보기 힘들다 (Choi, 2013). 18세기에 이르러서야 구체적 수치로 답을 구하는 과정을 기술하는 전통적인 방식에서 수학적인 근거를 토대로 계산법의 타당성을 제시하는 기술 방식으로의 변화가 나타났다고 할 수 있다. 특히, 18세기 후반에 저술된 <산학입문>, <주해수용>, <고사십이집> 산학서의 문제 풀이과정에서 수학적 논리가 엄밀해진 사례들을 다음과 같이 찾아볼 수 있다.
첫째, 이전 시기의 산학서와 동일한 문제에 대해서 동일한 풀이를 제시하면서도 풀이법의 수학적 근거를 추가적으로 설명하고 있는 경우이다. 대표적인 사례로 <고사십이집> 방전장의 Figure 3과 같은 원전(圓田) 문제를 들 수 있다. 저자 서명응이 제시하고 있는 풀이 ①, ②, ③은 <묵사집산법>과 <구일집>에서도 동일하게 제시되고 있는 원의 넓이 계산법이다. 다만, 저자 경선징과 홍정하는 문제에서 주어진 지름과 둘레의 구체적인 수치를 계산 공식에 대입하여 계산하는 절차를 기술하고 있을 뿐, 공식에 담겨진 원리에 대한 설명은 제시하지 않는다. 반면에 Figure 3에서 확인할 수 있듯이, <고사십이집>은 세 가지 풀이에서 각각 0.75, $\frac{1}{4}$, $\frac{1}{12}$를 곱하는 이유를 원의 넓이와 직사각형 넓이 사이에 성립하는 비를 사용하여 설명하고 있다. 원래 풀이 ①은 원주율로 고율(古律) 3을 사용했다는 것을 전제로 한 계산법으로, ‘$(원넓이) = (지름)^2 × \frac{3}{4} = (2r)^2 × \frac{3}{4} = (3r)^2 ≒ πr^2)$’으로 유도할 수 있다. 이때, ‘$(원넓이) = (지름)^2 × \frac{3}{4})$’이라는 계산식 구조는 원의 넓이가 한 변의 길이가 지름인 정사각형 넓이의 에 해당한다는 것을 직관적으로 파악하게 해준다. 이와 같이 원의 넓이를 직사각형의 넓이와의 관계 속에서 파악하는 것은 전통산학이 여러 가지 모양의 평면도형의 넓이를 구하기 위해서 이잉보허(以盈補虛)의 원리를 지속적으로 사용한 것과 연결된다. 이잉보허의 원리는 중국산학자 李淳風이 ‘남는 것으로 빈 곳을 채워 직사각형을 만드는 원리’라고 설명한 것으로, 출입상보의 원칙 또는 In Out Principle이라고 불리는 등적변형의 원리를 말한다 (Cha, 2004). Figure 4는 <고사십이집> 방전장에 실린 제전(梯田, 등변사다리꼴), 규전(圭田, 이등변삼각형), 구고전(勾股田, 직각삼각형)의 넓이를 직사각형의 넓이로 등적변형하여 설명하는 그림이다. 저자 서명응은 본문 설명에서 ‘이등변삼각형, 직각삼각형, 등변사다리꼴 모양의 넓이를 구할 때, 주어진 길이와 너비를 곱하면 모두 직사각형 넓이가 되므로, 직사각형의 넓이를 반으로 나누는 것이다. 등변사다리꼴 넓이는 먼저 길이(높이)나 너비(윗변아랫변)를 반으로 나누어 곱해도 된다’고 기술함으로써, 평면도형의 넓이 계산법이 성립하는 수학적 근거가 직사각형으로의 등적변형의 원리임을 분명하게 설명하고 있다.
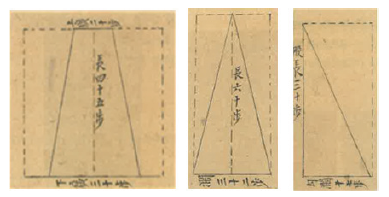
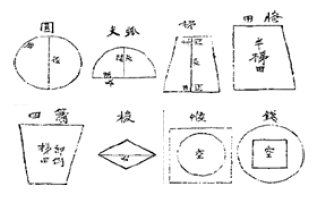
둘째, 수학적 논리의 엄밀성은 도형 그림을 삽입한 도해(圖解)를 통해 계산법을 직관적으로 이해하도록 돕거나 풀이의 타당성을 정당화하는 사례에서 찾아볼 수 있다. 도해를 통한 시각화는 이전 시기의 산학서와 비교할 때 눈에 띄는 변화 중의 하나이다. <묵사집산법>의 전무형단문은 여러 가지 모양의 평면도형의 넓이를 다루고 있지만, 도형 그림이 문제와 함께 제시되지는 않는다. 다만,’天’권의 본문이 시작되기 전인 맨 앞쪽에 도형 그림을 모아놓은 형식으로 전해내려올 뿐이며, 제시된 도형 그림은 길이나 너비, 꼭짓점 등의 도형의 구성요소들이 전혀 표기되지 않은 상태이다. <묵사집산법>보다 더 늦은 시기에 쓰여진 <구일집> 전무형단문에는 오히려 도형과 관련된 어떤 그림도 제시되지 않는다. 반면에 18세기 후반에 쓰여진 <산학입문>의 방전구적법에는 여러 가지 평면도형 이름 또는 땅 모양 이름에 도형 그림이 하나씩 대응되어 제시되어 있으며, 그 개수도 32개에 이른다. 특히, Figure 1과 Figure 5에서 확인할 수 있듯이, 제시된 그림에는 장(長, 길이)과 경(徑, 지름)과 같은 도형의 구성요소와 형태상의 특징이 표기되어 있다. 예를 들어, 소전(簫田)에는 사다리꼴을 거꾸로 한 도형(卽倒梯田)이라는 설명이, 장전(牆田)에는 사다리꼴의 반(半梯田)이라는 설명이 있으며, 후(帿, 정사각형 안에 원이 있는 도형)와 전(錢, 원 안에 정사각형이 있는 도형)에는 가운데가 비어 있다는 사실이 한자 공(空)으로 표기되어 있다. 이전 시기와 달리 평면도형 넓이를 구하는 문제에서 도형 그림을 함께 제시한 새로운 변화는 독자들로 하여금 도형의 넓이 계산법을 시각화한 도형 형태와 연결하여 보다 직관적으로 이해할 수 있도록 돕는 유용한 수학적 표상이라고 할 수 있다. 도형 그림과 그리기 활동이 도형 개념 학습을 촉진한다 (Kwon, 2021)는 측면에서도 의미있는 변화로 볼 수 있다.
한편, 동일한 시기의 <고사십이집>은 도형 그림을 단순히 평면도형의 형태만을 시각화하는 수준을 넘어 계산법의 타당성을 수학적으로 정당화하는 수단으로 사용한 산학서이다. 앞에서 살펴본 바 있는 Figure 4는 사다리꼴, 이등변삼각형, 직각삼각형의 넓이 공식이 직사각형으로 등적변형하는 원리에 의해 도출된다는 것을 시각화하여 보여주는 대표적 사례이다. 오늘날 기준으로는 단순하기 짝이 없지만, 이전 시기의 산학서 내용에서는 찾아볼 수 없는 보다 진화된 설명방식인 것은 부정할 수 없다.
다음 Figure 6은 <고사십이집> 구고팔선 단원의 직각삼각형과 관련된 문제에서 풀이에 추가되어 제시된 도해 사례이다. 위쪽 사례는 직각삼각형 甲乙丙을 중수선 甲丁으로 나누어 두 개의 직각삼각형을 얻고, 삼각형 甲乙丙의 乙丙과 甲乙의 비가 삼각형 甲丁丙의 甲丙과 甲丁의 비와 같고 삼각형 甲丁乙의 甲乙과 乙丁의 비와 같다는 비례관계로부터 높이 甲丁을 구할 수 있음을 제시한 그림과 함께 논리적으로 설명하고 있다. 아래 사례 역시 직각삼각형 甲乙丙과 丁戊丙의 닮음을 이용하여 戊丙과 甲乙의 비가 乙丙과 己庚의 비와 같다는 비례관계로부터 삼각형 甲乙丙에 내접하는 정사각형 己壬乙庚의 한 변의 길이 己庚을 구할 수 있음을 제시한 그림과 함께 논리적으로 설명한다. <산학입문>의 도형 그림에서 표기되지 않았던 각 점을 ‘甲, 乙, 丙, 丁, …’의 십간(十干)을 사용하여 표기한 것도 주목할 만하며, 상호 비례나 닮은 도형(同式形) 개념을 사용하여 설명하는 것도 이전 시기와 차별화되는 변화이다. 이전 시기의 산학서들이 풀이에서 계산 절차만을 기술한 것과 비교하면, 추가된 설명과 그림은 풀이에 사용된 알고리즘이 어떻게 유도되었는지를 엄밀하게 논리적으로 추론하고 정당화하는 역할을 한다. 다른 산학서에서 찾아보기 힘든 해법을 정당화하는 기술 방식과 도형 그림을 제시하는 표상의 변화, 닮은 도형과 같은 새로운 수학적 개념의 등장은 18세기 후반이라는 시대적, 사회적 배경을 반영한 것이며, 구체적으로 <수리정온> 등 중국산학서를 통해 유입된 서양수학의 영향으로 볼 수 있다.셋째, 수학적 사고의 엄밀성을 엿볼 수 있는 사례로 근삿값에 대한 인식이 분명해졌다는 것과 보다 정밀한 근삿값을 추구하는 경향을 들 수 있다. 대표적인 사례로 원주율과 그 근삿값에 대한 인식의 변화가 확인된다. 전통산학에서 원주율은 <구장산술>에서 제시한 고법(고율) 3을 비롯하여 劉徽의 휘율(휘술) $\frac{157}{50}$과 5세기 祖沖之의 밀률 $\frac{355}{113}$(때로는 약률 $\frac{22}{7}$)가 주로 사용되었다. <묵사집산법>을 비롯한 조선산학서에는 문제마다 고법, 휘율, 밀률 등 사용할 원주율 종류가 별도로 제시되어 있다. 그런데 한 가지 아쉬운 점은 이상의 원주율이 실제로는 근삿값임에도 불구하고, 시용하고 있는 원주율이 근삿값임을 설명한다든지 각 원주율의 정밀도 차이를 비교하거나 오차 여부를 설명하는 산학서를 찾아보기 힘들다는 점이다.
반면에 18세기 후반의 산학서에는 원주율의 근삿값에 대한 인식이 분명하게 드러난다. <산학입문>은 세 가지 원주율에 대해 <산학본원>을 보라고 하고 있는데, <산학본원>의 직빙원률에는 ‘구장산술에서 사용한 원주율 3이 참값에 미치지 못하는 값’이라는 것과 ‘약률($\frac{22}{7}$)이 간략하여 쓰기 편한 것이지 밀률의 정밀함에는 미치치 못한다’는 것을 밝히고 있다. <주해수용> 총례 방원승제율에도 ‘휘율과 밀률은 고법에 비하여 오차가 적어 정밀하지만 여전히 남고 부족함을 면하지 못한다. 대체로 휘률과 밀률은 고법 3의 간결함만 못하고 서양 원주율의 정밀함만 못하다. 배우는 자는 이에 대해 상세히 알아야 한다’는 문장이 있다. <고사십이집> 방전 수법에도 ‘고법을 사용하면 지름이 1인 원둘레가 3이라고 하지만 실제로는 지름이 1척일 때 원둘레는 3척보다 조금 크다. <수리정온>에는 지름이 1이면 원둘레가 3.14159265 남짓이라고 규정하고 있다’는 설명이 제시되어 있다. 세 산학서 모두 전통적으로 사용되어 온 고법, 휘율, 밀률 등의 원주율이 근삿값에 해당한다는 것을 인식하고 있음을 보여줄 뿐 아니라 고법의 간결함과 휘율과 밀률의 상대적 정밀함을 비교하고 있으며, 서양산술에서 다루고 있는 보다 정밀한 원주율을 소개하고 있다는 점에서 의미가 있다.
근삿값의 정밀함에 대한 인식이 드러나는 사례로 방오사칠(方五斜七)을 사용한 문제를 들 수 있다. <묵사집산법>의 포산선습문에 방사법(方斜法)으로 소개되어 있는 방오사칠은 정사각형의 한 변의 길이와 대각선의 비가 5:7이라는 것으로, 실제 길이의 비 $1:\sqrt{2}$를 근사적 비 1:1.4로 계산하는 방법이다. 저자 경선징은 揚輝로부터 나온 방사법이 정밀하지 않음을 포산선습문에 기술하고 있지만, 실제로 귀제숭실문의 여러 문제를 방오사칠을 적용하여 해결할 때는 결과가 근삿값에 불과하다거나 오차가 예상된다는 표현 없이 오히려 ‘문제에 합당한 답’이라고만 서술하고 있다. 반면에 <산학입문> 방전구적법의 방전중유상(方田中有桑)에서는 방오사칠 자체가 오답의 원인이라는 것과 아주 짧은 단위(자, 치)에서나 쓸 수 있는 것이지 백 무가 넘는 큰 단위에서는 오차로 인해 쓸 수 없음을 기술하고 있다. 이와 관련하여 <고사십이집>의 측정값의 수치 뒤에 나타나는 ‘약(弱)’ 또는 ‘유여(有餘)’등의 표현에 주목할 필요가 있다. 예를 들어, 삼척유여(三尺有餘)는 ‘3척보다 약간 크다’는 것을 나타내고, 육보약(六步弱)은 ‘6보보다 약간 작다’는 것을 뜻하는 표현이다. 이상의 사례들은 오늘날의 기준으로 보면 다소 사소하고 단순하지만, 이전 시기의 산학서에서 거의 볼 수 없던 설명과 표현이라는 측면에서 그 의미를 찾아볼 수 있다. 즉 18세기 후반의 산학서에서 근삿값에 대한 인식이 드러난다는 것과 오차가 적은 근삿값 사용으로 보다 정밀한 값을 추구하는 노력이 있었다는 것을 통해 참값에 대비한 근삿값의 한계 인식과 더불어 엄밀한 수학적 사고를 추구하는 경향을 보여주는 근거라고 할 수 있다.
구고를 확장한 삼각법과 팔선
18세기 후반 산학서에서 이전 시기에 다루지 않았던 새로운 평면도형 관련 주제가 소개되거나 다루어지는 사례가 확인된다. 대표적인 주제가 오늘날의 삼각비, 삼각함수에 해당하는 팔선(八線)이다. 이전 시기의 <구일집> 잡록에는 1713년(숙종 39년) 조선에 사신으로 온 중국 사력 何國柱와 저자 홍정하의 대담이 실려 있는데, 이 중에는 何國柱가 제기한 ‘지름 10자인 원에 내접하는 정오각형의 한 변과 넓이는 얼마인가?’라는 문제가 있다. 홍정하는 내접정오각형의 넓이는 원 넓이의 $\frac{5}{6}$라는 근삿값으로 쉽게 구하지만, 정오각형의 한 변의 길이는 구하지 못하였다. 何國柱는 이에 대한 해법으로 ‘한 변의 길이의 반(半弦)은 36도의 정현수(正弦數)’임을 이야기하는데, 오늘날 표현으로는 ‘정오각형의 한 변의 길이는 $2rsin36°$’에 해당한다. 이것이 바로 조선산학에서 삼각법 관련 내용이 최초로 등장하는 장면으로 알려져 있지만, 아쉽게도 <구일집>을 비롯한 18세기 전반의 산학서에서 삼각법에 대한 더 이상의 논의를 찾아볼 수 없다.
팔선(八線)이라고 불린 삼각법은 18세기 후반에 이르러 <주해수용>과 <고사십이집>에서 좀 더 정리된 형태로 재등장한다. <주해수용> 내편 下 팔선총률에서 다루는 팔선(八線)은 정현(正弦, $rsin\theta$), 여현(餘弦, $rcos\theta$), 정시(正矢, $r-rcos\theta$), 여시(餘矢, $r-rsin\theta$), 정절(正切, $rtan\theta$), 여절(餘切, $rcot\theta$), 정할(正割, $rsec\theta$), 여할(餘割, $rcosec\theta$)이다. 팔선총률에는 팔선사이의 관계를 이용하는 문제들이 실려 있는데, 그 중에 하나가 정현을 알 때 여현을 구하는 문제이다. 저자 홍대용은 구고현 관계 $고 = \sqrt{현^2 - 구^2}$를 이용하여, 정현 $rsin\theta$를 구, 반지름을 현으로 하여 고에 해당하는 여현 $rcos\theta$를 구하고 있다. 이 과정을 $rcos\theta = \sqrt{r^2-(rsin\theta)^2}$로 나타낼 수 있으며, 이 식은 다시 $cos\theta = \sqrt{1-sin^2\theta)}$가 됨을 의미한다. 이때, 여덟 개의 삼각함수는 정확한 정의가 기술되지 않은 상태로, 삼각함수 사이의 관계를 이용하는 예제들과 여러 가지 공식이 제시되고 있다는 한계가 있다.
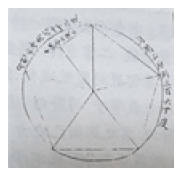
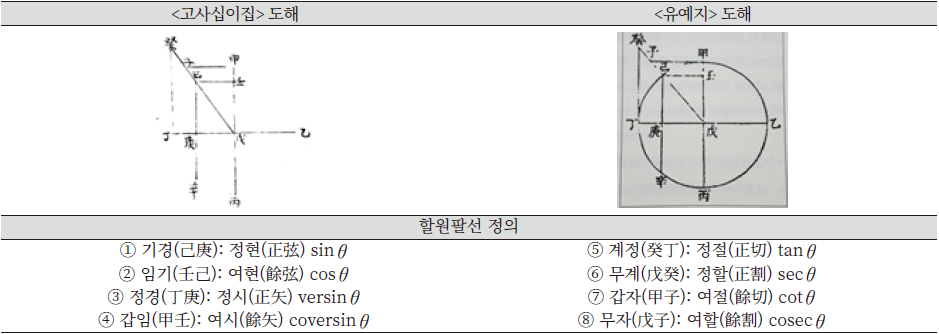
<주해수용>의 팔선이 어떤 보조 그림도 없이 예제만을 제시하는 방식이라면, <고사십이집>의 팔선은 여덟 개의 삼각함수를 기하적으로 표현한 선분 그림을 함께 제시함으로써 <주해수용>보다 체계적이고 논리적인 설명을 제시하는 경우이다. 원래 <고사십이집> 수예편은 전통적인 구고장 이름에 따라 각 단원을 명명하고 있으나, 마지막 구고 단원의 이름만은 ‘구고’가 아닌 ‘구고팔선’으로 명명했다는 특징을 가진다. 구고팔선에서는 먼저 직각삼각형 구고 관련 문제를 다룬 후에, 서양수학에 속하는 삼각함수의 정의를 할원팔선(割圜八線)으로 소개한다. Figure 8은 <고사십이집>에 실려 있는 팔선 그림으로, 왼쪽의 원문 도해에는 원 그림이 빠져 있는 반면에 서유구가 조부 서명응의 원문을 그대로 전사한 <유예지> 산법에는 원이 추가되었다는 차이가 있다.
<고사십이집> 원문에 따르면, 중심각 己戊丁을 정각($\theta$)이라 할 때 甲戊己는 여각(90° - $\theta$)이 된다. 이때 정각에 대응하는 호는 정호이고 여각 甲戊己에 대응하는 호는 여호이므로, 己丁은 정호이고 甲己는 여호가 된다. 이에 따라 정현부터 여할까지 총 8개의 할원팔선이 정의된다. 이 중에서 정시 $ver sin\theta$는 $1 - cos\theta$, 여시 $cover sin\theta$는 $1 - sin\theta$를 의미한다. 정현, 여현, 정시, 여시는 반지름이 1인 원의 경계 안에서 4선을 이루고, 정절, 정할, 여절, 여할은 반지름을 원의 경계 밖으로 연장하여 얻어진 4선에 해당하므로, 이를 합쳐 8선이라고 부른다.
저자 서명응은 단순히 팔선을 정의하는 데 끝나지 않고, 팔선의 기본적인 성질을 추가하여 설명한다. 예를 들어, 정호 己丁에 대한 餘(여현, 여시, 여절, 여할)가 여호 甲己에 대한 正(정현, 정시, 정절, 정할)이라는 것과 그 반대의 경우도 성립함을 부연하고 있다. 또한 도 이하의 각에 대한 팔선의 正과 餘는 도 이상의 팔선에서의 餘와 正으로 바꾸어 쓸 수 있으므로, 정각과 여각에 대한 팔선을 굳이 둘 다 구할 필요가 없음을 지적한다. 이 설명은 오늘날 표현으로, 인 삼각함수의 여각 관계를 의미한다. 뿐만 아니라 직각과 둔각의 팔선에 대해서도 예각과 구분하여 설명하고 있다. 예를 들어, $sin(90°-\theta) = cos\theta, cos(90° - \theta) = sin\theta$인 삼각함수의 여각 관계를 의미한다. 뿐만 아니라 직각과 둔각의 팔선에 대해서도 예각과 구분하여 설명하고 있다. 예를 들어, tan90°와 sec90°가 존재하지 않음에 대해서는 ‘癸丁과 戊癸가 평행하게 되어 점 癸가 존재하지 않으므로 정절과 정할이 정의되지 않는다’고 기술하고 있으며, 둔각에 대해서는 중심각 180°에서 둔각($\theta$)을 뺀 나머지 각도($180°-\theta$)의 팔선값을 이용한다고 기술한다. 이상은 학교수학의 삼각함수의 여각공식과 보각공식과 일치하는 설명이다. 다만, 둔각의 여현과 정절이 음수라는 것을 포함한 삼각함수 값의 부호에 대한 설명까지는 다루지 못한다는 한계가 있다. 그럼에도 불구하고 <주해수용>의 삼각법이 단지 관련 문제를 소개하고 계산하는 절차를 제시하는 수준인 반면에 <고사십이집>은 삼각함수에 대한 체계적 정의뿐 아니라 예각, 직각, 둔각에 이르는 삼각함수 값의 탐구, 정각과 여각의 관계에 대한 일반적인 설명을 제시한다는 것을 근거로 <주해수용>보다 높은 수준이라고 평가할 수 있다.
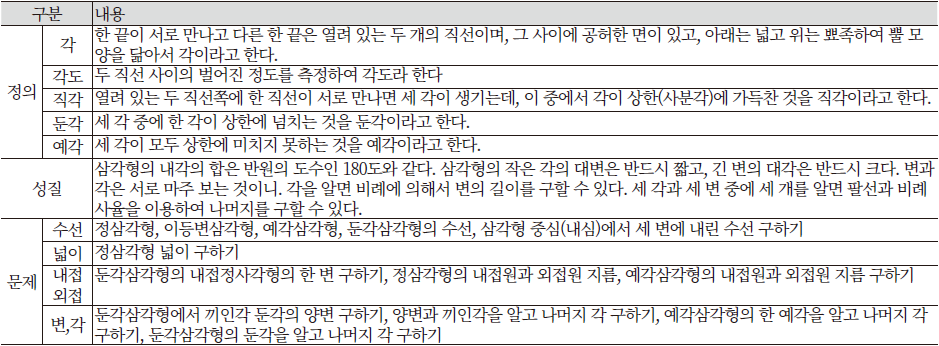
한편, <주해수용>은 팔선 이외에 평면도형과 관련된 새로운 주제를 다루고 있는데, 바로 삼각형의 구성요소 사이의 관계를 다루는 삼각총률이다. 이 단원은 팔선총률과 마찬가지로, 서양수학의 내용을 담고 있는 중국산학서 <수리정온>에 실려 있는 내용을 거의 그대로 기술한 것으로 보인다 (Chang, 2009). 삼각총률은 여러 가지 기하 개념의 정의와 도형의 성질로 시작하여 총 14개의 문제에 대한 일반적 풀이를 제시하고 있는데, 구체적인 내용은 Figure 9와 같다.
삼각총률에 담긴 모든 내용은 이전 시기의 조선산학서에서는 찾아볼 수 없는 것으로, 일단 각과 관련된 정의가 주목을 끈다. 오늘날 학교수학의 각의 정의 ‘한 점에서 그은 두 직선으로 이루어진 도형’과도 상당히 유사하며, 각(角)이라는 명칭을 생활에서 흔히 볼 수 있는 뿔 모양으로 설명하는 것도 흥미롭다. 또한 각의 크기에 따른 예각, 둔각, 직각의 분류와 수선, 대변, 대각 등의 새로운 용어의 등장은 비로소 조선산학에서 삼각형의 구성요소에 주목하게 되었다는 점과 보다 엄밀해진 정의를 추구하고 있다는 점에서 시대적 변화를 확인할 수 있다. 특히, 전통산학에서 삼각형의 변 사이의 관계가 직각삼각형에서만 한정적으로 다루어진 점과 비교하면, 삼각총률에서는 삼각형의 세 변과 세 각 사이의 관계가 일반 삼각형으로 확장되었다는 점에서 의의가 있다.
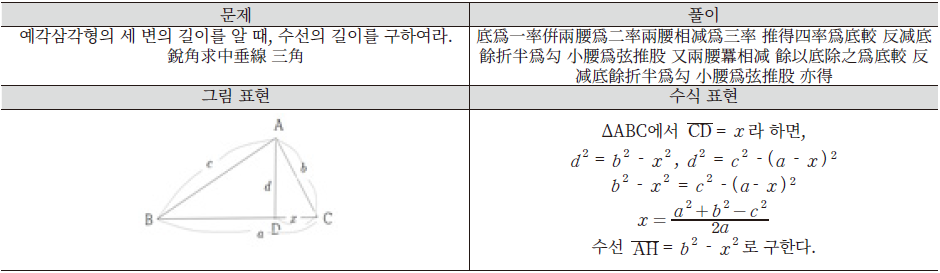
삼각형의 세 각의 합이 180도라는 점, 대각과 대변 사이의 크기 관계, 삼각함수와 비례식을 이용하여 삼각형의 여섯 가지 구성요소 중 세 가지가 주어진 경우에 나머지 변 또는 각의 크기를 구할 수 있다는 것은 오늘날 학교수학에서 삼각형을 다루는 방식과 유사하다. 특히, 여섯 가지 구성요소 중 세 각만 아는 경우는 세 변의 길이를 특정할 수 없다(只知三角則三線無準推法不行)는 사실도 부연 설명하고 있는 것을 확인할 수 있다. 이어지는 14개의 예제는 구체적인 수치 없이 특정한 변 또는 각의 크기를 구하는 일반적인 해법을 서술하고 있다. 예를 들어, Figure 10의 상단은 삼각총률에 제시된 예각삼각형의 수선의 길이를 구하는 문제와 풀이이고, 이 과정을 오늘날의 그림과 수식으로 나타내면 Figure 10의 하단과 같다.
제시된 풀이는 비례사율을 사용하여 비례식 ‘$a : (c + b) = (c - b)$’을 통해 저교(底較)를 구한 다음, 밑변 a에서 저교를 뺀 값의 반인 $\overline{CD}$선분를 구하고, 구고법을 이용하여 수선 $\overline{AH}$를 구하는 방식이다. 이 과정을 오늘날 수식과 비교하면 해법의 타당성을 확인할 수 있다.
결론
본 논문은 중국을 통해 서양수학이 본격적으로 유입된 18세기 후반에 저술된 조선산학서에 나타난 기하 영역 의 변화를 살펴보았다. 특히, 18세기 조선산학서의 대수 영역에 나타난 서양수학의 표현 및 계산법의 변화를 살펴본 기존 연구를 연계・심화하여 18세기 후반의 조선산학서에서 평면도형과 관련된 내용들이 이전 시기와 비교하여 어떻게 차별화되어 다루어지고 있는지를 분석하였다. 이를 위해 본 연구에서는 18세기 후반에 저술된 서명응의 <고사십이집>과 황윤석의 <산학입문>, 홍대용의 <주해수용>을 분석의 중심 문헌으로 선정하여 살펴본 연구 결과는 다음과 같다. 먼저 <고사십이집>, <산학입문>, <주해수용>의 평면도형과 관련된 일부 문제에서 이전 시기의 조선산학서에는 찾아볼 수 없는 계산법과 설명의 변화를 확인할 수 있었다. 첫 번째 변화는 측정 대상으로서 도형이 아니라 도형의 구성요소와 성질에 주목하는 탐구 대상으로 접근하는 설명이 등장했다는 점이다. 본 연구에서는 선행연구 (Chang, 2009; Choi, 2013)에서 근거로 제시한 <산학입문>의 ‘방전구적법’ 사례에 <주해수용>의 면적법(面積法) 단원을 추가로 제시하였다. 면적법 단원은 땅의 넓이를 구하는 양전법 단원과 달리, ‘평면의 넓이를 구하는 것(面積者 平面之積)’으로 설명되고 있었으며, 도형 이름 또한 평면을 뜻하는 ‘면(面)’을 사용한 정방면, 장방면, 원면, 삼각면이었다. 또한 평면도형을 전통적인 땅의 모양이 아니라 보다 상징적인 한자 모양과 대응시켜 설명하고 있었는데, 이 과정에서 제시된 단위 넓이에 대한 설명 또한 의미있는 사례였다. 이러한 변화에 대해서 도형을 실생활 맥락의 땅(田)이라는 사물의 모양으로 인식했던 단계에서 보다 추상화된 평면도형으로 개념화하는 단계로 발전해가는 과정 중에 있다고 해석하였다.
계산법 변화의 두 번째 양상은 서양수학의 계산법인 서법(西法)을 별해로 추가 제시한 사례에서 찾아볼 수 있었다. 대표적으로, <고사십이집>에서 구고의 넓이는 전통적인 계산법 이외에, <수리정온>의 영향을 받은 중수선(中垂線)을 사용한 방법과 헤론의 공식을 추가로 제시하고 있었다. 계산법 변화 양상은 서양수학의 계산법이 반영되어 기존 풀이법을 대체한 사례에서도 확인되었는데, 대표적으로 서양의 비례사율이 전통적인 금유술을 대신한 사례를 들 수 있었다. 이와 같은 설명과 계산법 변화 사례는 중국한역서를 통해 접하게 된 서양수학 내용을 18세기 후반이라는 시대적 배경 속에서 저자 개인이 자체적으로 해석 연구하여 수용한 경우로, 수학이 점진적으로 형식화되고 발전해가는 모습뿐 아니라 사회문화적 요인에 영향을 받는 인간적이고 역동적인 활동임을 인식시키는 데 유용한 자료로 활용될 수 있다.
다음으로, 수학적 논리의 엄밀성 측면에서도 이전 시기와 다른 변화 사례를 확인할 수 있었다. 18세기 후반에 쓰여진 세 권의 산학서에서는 구체적 수치로 답을 구하는 과정을 기술하는 전통적인 방식과 함께 일부 문제에 대해서 수학적 근거를 토대로 계산법의 타당성을 기술하는 새로운 방식이 공통적으로 관찰되었다. 수학적 논리가 보다 엄밀해진 사례는 이전 시기의 산학서와 동일한 문제 풀이를 제시하면서도 풀이법의 수학적 근거를 추가적으로 제시하고 있는 <고사십이집> 방전장에서 분명하게 드러나고 있었다. <고사십이집>은 세 가지 원의 넓이 공식에 담긴 수학적 원리를 원의 넓이와 직사각형 넓이 사이에 성립하는 비를 사용하여 설명하고 있었으며, 평면도형의 넓이 계산법을 직사각형의 등적변형으로 일관성 있게 설명하였다. 이에 대해 계산법 원리가 성립하는 근거를 수학적 논리로 엄밀하게 설명하고자 하는 시대적 변화를 보여주는 사례라고 판단하였다.
18세기 후반의 산학서에 나타나는 도해를 통한 시각화 또한 수학적 엄밀성의 대표적인 사례였다. 도형 그림을 삽입한 도해(圖解)는 이전 시기의 산학서에서는 찾아볼 수 없는 변화로, 풀이에 사용된 계산법을 직관적으로 이해하도록 돕거나 풀이의 타당성을 정당화하는 역할을 하고 있었다. <산학입문>의 방전구적법에 제시된 32개에 이르는 도형 그림과 도형의 구성요소와 형태상의 특징이 표기된 사례, <고사십이집>의 계산법의 타당성을 수학적으로 정당화하는 수단으로 도해를 제시한 사례가 대표적이었다. 또한 구고팔선 단원의 직각삼각형과 관련된 문제에서 풀이에 추가 제시된 도해의 경우에는 각 점을 ‘甲, 乙, 丙, 丁, …’을 사용하여 표기하고, 상호 비례나 닮은 도형(同式形) 개념을 사용하여 설명하는 등 이전 시기와 차별화되는 변화를 보여주었다. 수학적 사고의 엄밀성을 추구하는 변화는 근삿값에 대한 명확한 인식과 보다 정밀한 근삿값을 추구하는 경향에서도 찾아볼 수 있었다. 18세기 후반의 세 권의 산학서는 전통적으로 사용되어 온 고법, 휘율, 밀률 등의 원주율이 근삿값에 해당한다는 것을 밝히고 있을 뿐 아니라 고법의 간결함과 휘율과 밀률의 상대적 정밀함을 비교하고 있으며, 서양 수학에서 다루고 있는 보다 정밀한 원주율을 소개하고 있다는 점에서 의미가 있었다. 또한 ‘약(弱)’ 또는 ‘유여(有餘)’ 등의 측정값의 표현에서도 살펴볼 수 있었다. 오늘날 기준으로 보면 당연하고 사소한 표현들에 불과하지만, 이전 시기의 산학서에서 찾아보기 힘든 설명들이라는 측면에서 수학적 사고가 점차적으로 엄밀해지고 형식화되고 있음을 보여주는 근거라고 볼 수 있다. 이상의 사례는 그동안 사고의 자동화로 인해 당연시했던 수학적 아이디어들을 재음미하는 기회를 부여함으로써 보다 의미있는 사고활동을 가능하게 한다는 수학사의 역할을 실감하게 해준다.
마지막으로, 18세기 후반 산학서에서 이전 시기에 다루지 않았던 새로운 기하 영역 주제가 등장한 것을 확인할 수 있었다. 오늘날의 삼각비, 삼각함수에 해당하는 팔선(八線)은 이전 시기의 <구일집> 잡록의 대담에서 짧게 용어만 언급되었던 것으로, 18세기 후반에 이르러서는 <주해수용>과 <고사십이집>에서 좀 더 정리된 형태로 다루어지고 있었다. 특히, <고사십이집>의 팔선은 여덟 개의 삼각함수에 해당하는 선분을 원을 분할한 그림과 함께 제시함으로써 <주해수용>보다 체계적이고 논리적인 설명을 제시할 뿐 아니라, 삼각함수의 여각공식과 보각공식에 해당하는 팔선의 기본적인 성질을 추가하여 설명하고 있었다. 삼각함수에 대한 체계적 정의뿐 아니라 예각, 직각, 둔각에 이르는 삼각함수 값의 탐구, 정각과 여각의 관계 등 삼각함수의 일반적 성질을 논하는 수준에 이르렀다고 평가할 수 있다.
삼각형의 구성요소 사이의 관계 또한 18세기 후반 산학서가 새롭게 다룬 평면도형 관련 주제이다. <주해수용>의 삼각총률은 각과 각도의 정의부터 시작하여 각의 크기에 따라 예각, 둔각, 직각을 수학적으로 정의하고 있으며, 수선, 대변, 대각 등의 새로운 용어를 사용하고 있었다. 또한 삼각형의 세 각의 합이 180도라는 성질, 대각과 대변 사이의 크기 관계, 삼각형의 여섯 가지 구성요소 중 일부를 알 때 나머지를 구하는 방법들을 다루고 있었다. 특히, 삼각총률은 삼각형의 세 변과 세 각 사이의 관계를 직각삼각형에서 일반 삼각형으로 확장했다는 의의가 있었다. 물론 이상의 내용들은 중국산학서 <수리정온>에 실려 있는 내용을 거의 그대로 기술한 것으로 보이지만, <수리정온> 자체가 유럽의 대수학과 삼각법을 한역한 산학서라는 면에서 조선산학이 서양수학의 이론적이고 논증적인 전개 양식을 점진적으로 수용하는 과정이라고 볼 수 있다.
물론 이상의 분석 결과가 분석대상인 세 권의 산학서에서 공통적으로 관찰되는 변화는 아니다. 예를 들어, 삼각법과 팔선은 <주해수용>과 <고사십이집>에서는 다루고 있으나 <산학입문>에서는 찾아볼 수 없다. 그렇지만 <산학입문>은 두 산학서가 다루지 않는 각 평면도형의 구성요소와 특징 등을 그림을 제시하여 설명하고 일반화에 이르기도 한다. 이와 같은 현상은 저자 개인의 수학적 안목과 산학 문헌의 집필 의도가 다르기 때문이라고 볼 수 있다. 18세기 후반의 조선산학서 중에서 <산학입문>은 평면도형의 탐구와 일반화된 설명, 근삿값에 대한 인식 측면에서 의미가 있으며, <주해수용>은 삼각총률과 팔선총률을 통해 서양수학의 수용을 보여주고 있다는 점에서 의미가 있다. 마지막으로 <고사십이집>에 대해서는 근삿값의 정밀성에 대한 논의, 등적변형에 기반한 평면도형의 넓이 계산법의 원리 설명, 도해를 통한 해법의 정당화, 서양수학을 수용한 다양한 계산법 제시와 새로운 삼각함수 팔선에 대한 설명 등 전체적으로 저자 서명응의 수학적 안목과 학문적 수준을 높이 평가할 수밖에 없다.
수학의 역사는 그동안 그 이유나 방법에 대해 의문조차 갖지 않고 당연하게 생각했던 수학 개념과 법칙, 아이디어들을 재음미하는 기회를 부여함으로써 보다 의미 있는 사고활동을 가능하게 한다 (Arcavi, 1991; Woo, 1998). 본 연구에서 제시된 조선산학의 사례들은 오늘날 학교수학에서 사고의 자동화로 인해 당연시되어 사고의 대상이 되지 못했던 수학 내용과 계산법을 다시 한번 재검토하게 하는 자료로 활용될 수 있을 것이다. 예를 들어, 보다 정밀한 원주율의 근삿값을 찾아가는 기나긴 여정, 평면도형의 넓이를 단순히 공식을 암기하여 적용한 것에서 점차 도해를 통한 등적변형 원리로 정당화하는 과정, 직각삼각형에 내접하는 원의 반지름을 구하는 방법이 서양수학의 수용으로 보다 풍부해진 사례에 대해 학교수학과 비교하게 하거나 오류를 찾게 하는 활동을 할 수 있다. 본 연구는 조선산학이 중국을 비롯한 다른 문화권의 수학지식을 수용하여 자체적으로 발전시킨 과정을 거쳐왔다는 것을 18세기 후반의 조선산학서에 나타난 수학적 사례들을 통해 드러내고자 하였다. 특히, 18세기 후반은 조선산학이 기하를 탐구하고 추론하는 대상으로 접근했다는 것과 수학적으로 엄밀성을 추구했다는 점에서 이전 시기와 구분되는 새로운 수학적 단계로 진전하고 있었다는 점을 확인하였다는 점에서 의의가 있다. 또한 기존의 선행연구들이 조선산학의 추론과 정당화 시기를 19세기 산학서를 기준으로 삼았던 것과 비교하여, 본 연구에서는 최소한 18세기 후반으로 앞당기는 사례를 제시하였다.
본 연구는 다만 조선산학이 점진적으로 엄밀해지고 형식화되어가는 모습을 평면도형 관련 내용에 한정하여 부분적으로 확인했다는 한계를 가진다. 앞으로 본 연구 결과를 기초로 하여 조선산학의 다양한 주제에 대한 연구가 지속적으로 이루어지기를 기대한다.