A study on the mathematics curriculum for elementary school in Korea to improve teaching of chance

서론

통계적 자료에 기반을 둔 판단과 의사결정, 불확실성에 대한 대처와 사회 현상의 예측과 이해가 중요한 현대 사회의 흐름에 따라 학교수학에서 확률교육의 중요성이 점점 커지고 있다. 최근 확률의 지도와 관련하여 수학과 교육과정에서 큰 변화가 있어 왔다. 2009 개정 교육과정에서는 확률의 정의를 초등학교에서 중학교로 상향 조정하고 확률의 직관적 개념으로서 ‘가능성’을 초등 5~6학년군에서 지도하는 변화가 있었다(MOEST, 2011). 또한 2015 개정 교육과정에서부터 초등학교 수학의 ‘확률과 통계’라는 영역명이 ‘자료와 가능성’으로 변경되었다(MOE, 2015). 확률을 ‘가능성’으로 변경한 것은 우연과 무작위성이라는 아이디어를 다루는 확률 개념이 가능성을 수량화하는 경험을 통해 발달해 왔다는 배경을 반영한 것이라 할 수 있다. Pfannkuch와 Ziedins (2014)에 따르면 확률 지도의 목표는 학생들이 비결정론적인 관점에서 세상을 바라보고 무작위성과 불확실성이 내포된 상황에서 의사결정에 필요한 사고를 개발하는 것이다. 이는 확률교육에서 학생들이 무작위성 아이디어를 이해할 수 있도록 지도할 필요가 있음을 시사한다.

최근 확률교육의 방향은 크게 세 가지로 요약될 수 있다(Ko & Hwang, 2020). 첫째, 고전주의적 접근에 국한되어 확률 개념을 지도하는 것을 지양하고 빈도주의적 접근의 지도를 강화할 것을 강조한다. 둘째, 학생들이 확률의 모델링 활동을 경험할 것을 강조한다. 확률의 모델링 활동을 통해 학생들은 우연과 무작위성 개념을 사회 현상이나 자연 현상으로까지 확장하는 사고의 토대를 마련할 수 있다. 셋째, 통계와의 관계에 주목하여 확률을 지도할 것을 강조한다. Schupp (1982)는 “확률 없는 통계는 장님과 같고 통계 없는 확률은 빈껍데기에 불과하다”(Eichler & Vogel, 2014, p. 87에서 재인용)고 언급하면서 확률과 통계의 지도가 상호보완적으로 이루어져야 함을 강조하였다. Burrill과 Biehler (2011)는 확률교육에서 자료 기반의 접근을 중요시하였으며, Eichler와 Vogel (2014)은 통계적 문제해결 과정에서 확률의 역할이 무엇인지 숙고함으로써 확률에 대한 이해가 깊어진다고 주장하였다. 이러한 확률교육의 변화 방향은 확률을 지도할 때 자료를 다루는 경험과 무작위성 개념을 개발할 수 있는 경험이 제공되어야 함을 시사한다.

지금까지 우리나라 초등학교 수학에서 가능성 지도에 대한 연구는 초등학교 수준에서 가능성 지도에 적합한 활동에는 어떠한 것이 있는지(Chang, 2020), 가능성 지도에 대한 국외 교육과정은 어떠한지(Chang et al., 2021; Park et al., 2014), 확률 내용의 역사적, 논리적, 심리적 측면 분석(Chang, 2013), 초등학생의 확률 개념 이해 조사(Yoon & Lee, 2011) 등이 주를 이루었다. 이들 연구는 주로 확률에 대한 고전주의적 관점에 국한되어 논의가 이루어졌다. 이에 최근 확률에 대한 고전주의적 관점을 탈피하여 확률을 어떻게 지도할 것인지에 대한 논의가 이루어지고 있다. 예를 들어, Lee 외 (2019)는 자료에 기반을 둔 확률 개념 학습에 적합한 학습 경로를 설정하는 데 필요한 기초 자료를 제시하고자 시도하였다. 이들은 자료에 기반을 둔 확률 개념 학습 과제를 이용해 초등일반학생들과 초등수학영재학생들의 학습 양상을 비교, 분석하였다. 중심에 의한 추론과 변이성에 대한 추론을 분석의 두 축으로 하여 분석한 결과, 일반 학생들의 절반 정도가 경향성을 파악하는 수준의 사고를 보였으나 우연변이성의 인식에는 실패하는 보습을 보였다. 즉, 가능성을 지도할 때 학생들이 자료의 변이성으로 표출되는 우연 속성에 대한 이해가 이루어질 수 있도록 유념해야 함을 확인할 수 있다.

본 연구에서는 확률 현상을 이해하는 데 필요한 핵심 개념이자 확률적 사고 발달의 주된 요소인 우연(chance)과 무작위성(randomness)을 바탕으로, 우리나라 초등학교 수학과 교육과정 및 교과서에서의 가능성 지도 방식과 과제를 비판적으로 살펴보고, 확률교육의 기초로서 가능성 지도를 위한 개선 방안에 대하여 논의한다. 구체적인 연구 문제는 다음과 같다.

1. 가능성 지도의 목표가 확률적 사고의 발달이라는 점을 고려하였을 때, 우리나라 초등학교 수학에서 가능성 지도와 관련한 문제점은 무엇인가?

2. 1에서 확인된 문제점을 해결하기 위한 가능성 지도의 개선 방안은 무엇인가?

이론적 배경

우연 개념의 이해

우연을 뜻하는 단어 chance는 ‘떨어지다’라는 뜻을 지닌 라틴어 cadere로부터 파생된 것으로 명사형 cadentia는 사건이 발생함(falling out)이나 물건이 떨어지는 방식, 운, 경우를 의미한다(Reith, 1999). 우연은 필연의 반대로도 받아들여지는데, 일의 결과가 반드시 그렇게 될 수밖에 없는 것이 필연이라면, 우연은 그렇게 되지 않을 수 있었음에도 불구하고 충분한 이유 없이 그렇게 된 것을 말한다(Takeuchi, 2010).

Kuki (1985)는 우연을 정언적 우연, 이유적 우연, 인과적 우연 등으로 구분한다. 예를 들어, ‘삼각형의 세 내각의 합은 180도이다’는 삼각형 개념으로부터 세 내각의 합이 180도라는 사실이 연역적으로 도출되는데, 이는 개념과 속성의 관계가 필연적임을 뜻한다. 개념과 속성의 관계가 필연적이지 않은 것이 정언적 우연이다. 이유적 우연이란 어떤 현상이 발생하는 이유와 그 결과 사이에 필연적인 관계가 결여된 것을 말한다. 인과적 우연이란 ‘일어나는 일, 또는 일어난 일에 대해 과학적 논리적 필연성이 보이지 않는 사상(事象)’을 의미한다. Takeuchi (2010)는 인과적 우연을 확률과 통계와 관련하여 우리가 주목해야 할 우연으로 보고 있다.

확률과 통계가 수학의 다른 분야와 구별되는 특징은 이와 같은 인과적 우연에 대한 정의에 반영된다. 논리적인 필연성이 보장되는 연역적 사고에 기반을 두는 수학과 달리 확률과 통계는 일어나는 일 또는 이미 일어난 일 등 경험에 기반을 두는 귀납적 사고에 기반을 둔다.

단어 chance는 오늘날 가능성이라는 의미로도 사용된다. 이는 우연 상황에서 특정 사건이 일어날 것이라 기대하는 정도를 의미하는 단어로 가능성을 사용하는 것과 무관하지 않다. 가능성(chance)과 확률(probability)에 대해 기술한 저작에서 쿠르노(Antoine A. Cournot, 1801-1877)는 불어 chance와 probabilité를 서로 다른 두 개념을 지칭하는데 사용한다. probabilité는 진실성 또는 합리적 믿음의 정도를 의미하는 단어로 사용한 데 반해, chance는 해당 사건이 발생할 수 있는 용이성(facility)을 지칭하기 위해 사용하였는데 이는 주로 사건의 발생 빈도를 고려한 접근과 관련이 있다(Ko & Hwang, 2020). 푸아송(Siméon D. Poisson, 1781-1840)도 이와 유사하게 probabilité는 확률에 대한 주관적 사고 방식을 의미할 때, chance는 객관적 사고 방식을 의미할 때 사용하였다(Hacking, 1990). 이는 오늘날 확률의 정의가 관찰로부터 얻어진 사건의 빈도에 근거하여 정의하는 객관주의적 확률과 믿음의 정도로 정의하는 주관주의적 확률, 이렇게 크게 두 가지로 통용되는 모습에 그대로 반영된다(Stigler, 1986).

무작위성과 우연

우연과 무작위성 아이디어를 다루는 확률 개념이 가능성을 수량화하는 경험을 통해 발달해 온 것은 ‘우연’과 ‘가능성’이 동일한 단어(chance)를 사용하는 것과 무관하지 않다. 무작위성과 우연 개념의 관련성을 이해하는 것은 확률과 통계를 학습하는 데 필수적이다(Ko & Lee, 2010). 우리는 보통 개개의 결과들은 불확실하지만 여러 번의 반복 시행 결과는 일정한 패턴을 지니는 현상을 가리켜 무작위 사건이라 한다(Moore, 1990, p. 98). 개별적인 결과들의 불확실성은 우연 현상의 가장 큰 특성이며, 여러 번의 반복 시행 결과가 일정한 패턴을 지니는 것은 사건의 발생에 무작위성이 포함되어 있기 때문이다.

확률의 발달은 등확률의 원리가 필수적이었던 우연 게임과 밀접한 관련이 있었다는 점에서, 확률의 이론적 발달과 함께 무작위성 개념은 등확률성(equal likelihood)과 밀접하게 연결된다(Batanero & Serrano, 1999, p. 558). 1600년대 초에 갈릴레오(Galileo Galilei, 1564-1642)는 ‘동일한 확률’이라는 개념을 이해하고 이로부터 공정한 주사위 모형을 제안하였는데, 이것이 오늘날 우리가 사용하는 주사위의 모체이다. 정육면체 주사위는 각 방향에 대해 대칭적 구조를 가지고 있을 뿐만 아니라 균일한 재질로 만들어져 있어 바닥에 굴렸을 때 각 면이 나올 확률은 같다. 즉 모든 가능한 결과들은 1부터 6까지의 숫자들로 이루어진 균일확률표본공간을 형성한다(Ko & Lee, 2010). 이렇게 모든 가능한 결과들이 같은 확률로 나타나는 확률분포 상태를 가리켜 ‘균일분포’라 부르기도 한다(Bennett, 1998).

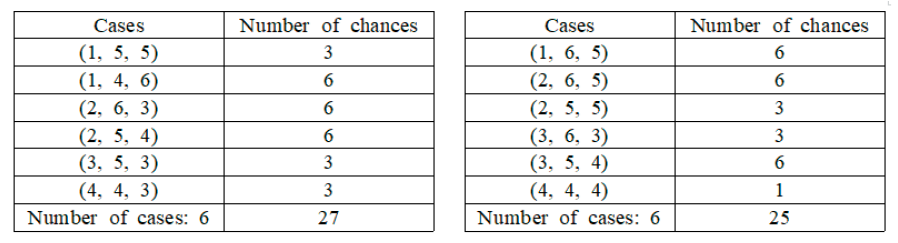
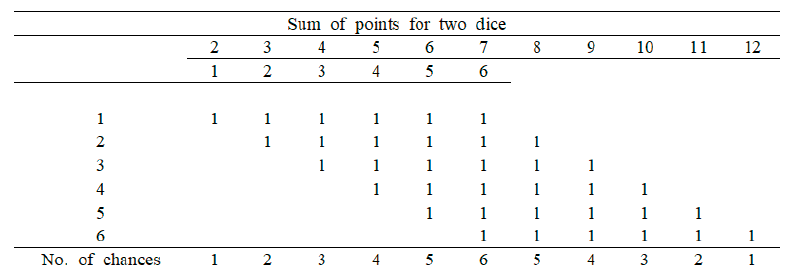
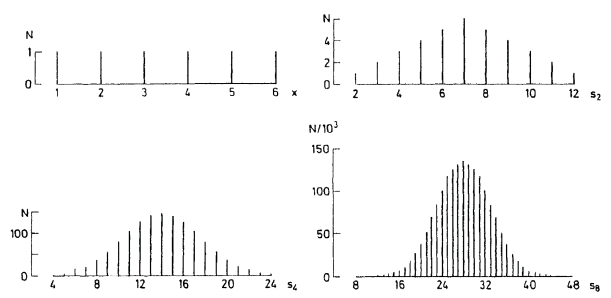
과거 사람들은 주사위 세 개를 던져 나온 눈의 수의 합에 내기를 걸었다. 눈의 수의 합이 3부터 18까지로 16가지이지만 가장 큰 값과 가장 작은 값은 거의 나오지 않고 11이나 12와 같은 중간에 있는 값들은 자주 나오기 때문에 16가지에 대해 가능성이 같지 않다고 생각했다. 그런데 사람들은 주사위 세 개를 던져 나온 눈의 수의 합 가운데 어떤 특정한 경우들은 나올 가능성이 같은데, 전문 도박사들이 항상 특정한 수에 내기를 거는 것에 의문을 가졌다. 예를 들면, 11이 나오는 경우는 (1, 5, 5), (1, 4, 6), (2, 6, 3), (2, 5, 4), (3, 5, 3), (4, 4, 3)로 6가지, 그리고 12가 나오는 경우 역시 (1, 6, 5), (2, 6, 4), (2, 5, 5), (3, 6, 3), (3, 5, 4), (4, 4, 4)로 6가지인데 왜 전문 도박사들은 항상 11에 내기를 거는지 궁금해했다. 주사위 세 개의 눈의 합이 11과 12인 경우는 모두 겉보기 경우의 수가 6가지로 동일하여 나올 가능성이 같은 것처럼 보이지만, 실제 경우의 수는 각각 27과 25로 분명히 다르다(Figure 1 참조). 제아무리 도박사라 해도 주사위 2개를 던졌을 때 눈의 합과 주사위 3개를 던졌을 때 눈의 합에 대한 문제는 카르다노(Girolamo Cardano, 1501-1576)와 갈릴레이에 의해 해결되었다. 그 이상의 주사위에 대한 문제는 매우 복잡한데 몽모르(Pierre R. Montmort, 1678-1719)는 2~9개의 주사위를 이용했을 때 눈의 수의 합의 분포표를 만들었다. Figure 2는 두 개의 주사위를 이용했을 때 눈의 수의 합에 대한 분포표이다. 이 이원표는 첫 번째 주사위의 눈의 수와 두 번째 주사위의 눈의 수를 연속적으로 결합해서 얻어지는 36가지의 경우의 수에 대한 분포를 나타낸다. 각각의 열에 있는 경우의 수를 더하면 각각의 합에 대한 경우의 수를 얻게 된다(Ko & Lee, 2010). 주사위 2~9개에 대한 몽모르의 이러한 발견은 중심극한정리를 설명하는 최초의 수치적인 예가 된다. Figure 3은 몽모르가 주사위 1, 2, 4, 8개를 사용했을 때 주사위 눈의 합에 대한 분포표를 그래프로 나타낸 것이다. 이와 같이 무작위 사건이 분포와 연결되면서 무작위성은 단지 각각의 자료가 아니라 자료집합 전체가 갖는 특성으로 이론화되었다(Hald, 2003).

Figure 1. The numbers of chances when the sums of points by throwing three dice are 11 and 12.

Figure 2. Montmorn's distribution table for the sum of points for two dice (Hald, 2003, p. 205).

Figure 3. Graphs of Montmort’s distribution of sums of points by throwing one, two, four, and eight dice (Hald, 2003, p. 210).

가능성 관념과 확률적 사고

확률 과제에 대한 아동의 반응을 심리학적으로 분석한 Piaget와 Inhelder (1975)에 따르면, 일반적으로 아동은 7~8세 시기에 우연과 필연을 구분하고 직관적 수준에서 우연을 인식함으로써 가능성 관념이 발달한다. Fischbein (1975)은 그보다 이른 시기인 학령기 이전에도 확실한, 불가능한, 가능한 사건을 구별하고 간단한 사건에 대해서는 우연 속성과 가능성을 파악할 수 있다고 주장하였다. 비록, 확률적 사고의 태동 시기에 대해서는 연구자들 사이에 차이가 존재하지만, 우연에 대한 인식이 확률의 초기 관념인 가능성에 대한 사고를 이끎으로써 확률적 사고의 토대를 마련한다는 생각은 공통적으로 드러난다고 볼 수 있다.

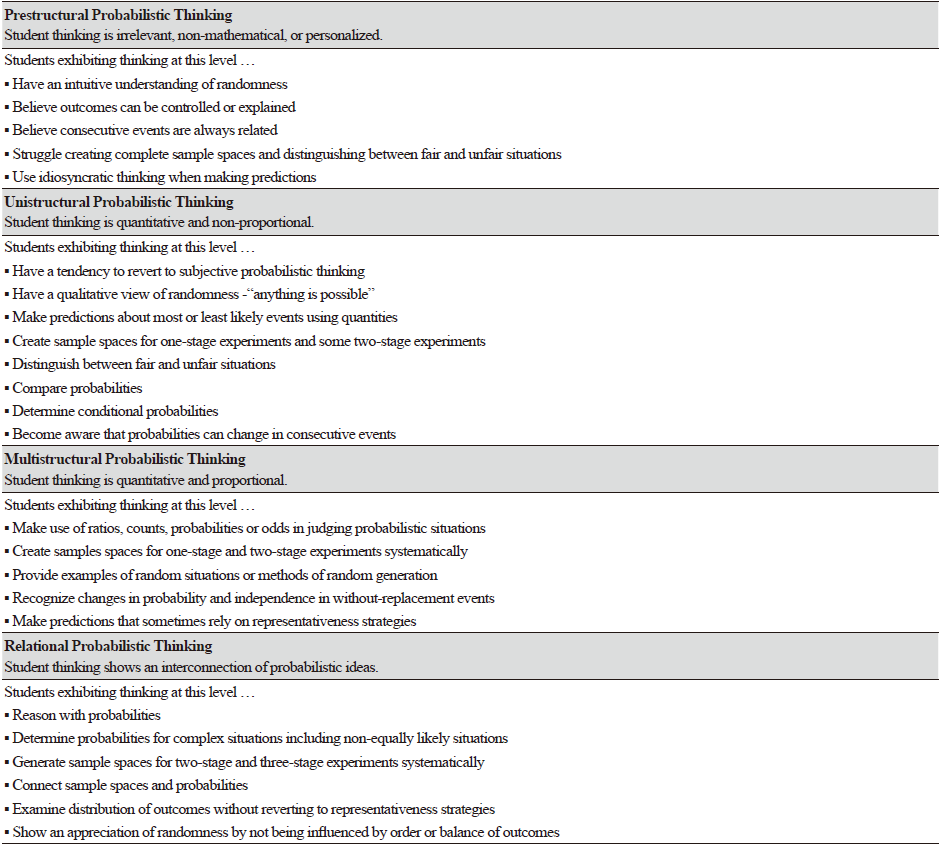
우연에 대한 인식이 가능성 관념의 발달로 이어지기는 하지만, 가능성 관념이 온전한 수준의 확률로 완성되려면 진실성과 합리성에 기반을 둔 추론을 통해 가능성 관념을 논리적으로 강화해야 하는 과정을 거쳐야 하는데, 이러한 강화 정도에 따라 확률적 사고의 발달 수준이 구별된다. 예를 들어, Jones 외 (1997)는 단일 사건의 가능함과 불가능함을 구분하는 제1수준부터 사건에 수치적 확률을 할당하는 제4수준에 이르기까지 총 4가지 수준으로 확률적 사고를 구분하여 제시하기도 하였다. 그 외에도 조건부확률, 무작위성, 등확률성 등 확률과 관련된 다양한 속성과 개념에 대한 이해를 바탕으로 확률적 사고의 수준 체계를 만들고자 했던 선행연구가 있었는데(Tarr & Jones, 1997; Watson et al., 1997, etc), Mooney 외 (2014)는 이를 종합하여 학생들의 확률적 사고 발달을 개괄적으로 살펴볼 수 있는 4수준 틀을 Table 1과 같이 제시한 바 있다(p. 502).

수준 체계에 비추어볼 때, 확률적 사고는 사건 결과에 대한 변이성을 바탕으로 우연 현상을 인지하는 아동의 직관으로 시작하여 점차 상황 정보를 기반으로 한 추론으로 나아가는 것으로서 그 수준이 발달한다고 볼 수 있다. 이때, 확률적 사고가 전 구조화된 수준에서 관계적 수준으로 나아가기까지는 무작위성에 대한 인식이 매우 중요한 요소로서 작용하고 있다. Table 1에서의 확률적 사고 발달에는 무작위성에 대한 모호하고 직관적인 인식에서 벗어나 이를 양화하고 일정한 질서를 발견하여 이를 기반으로 한 추론이 이루어지는 일련의 과정이 드러나 있다. 즉, 우연 사건의 반복 시행을 통해 획득한 자료에서 무작위성에 의한 정규적인 패턴을 찾고 이에 근거를 두어 변이성 추론을 통해 사건의 가능성을 예측하는 것이 확률적 사고의 본질적인 속성이다.

Table 1. A framework of probability thinking (Mooney et al., 2014, p. 502).

2015 개정 수학과 교육과정에서는 초등학교 가능성 지도의 의의로서 “사건이 일어날 가능성을 수치화하는 경험은 확률의 기초가 된다(MOE, 2015, p. 27)”고 명시하고 있다. 이는 초등학교 수학에서 가능성 지도는 단순히 가능성 관념의 현상에서 머무르는 것이 아니라 확률적 사고의 발달을 위한 토대로서의 역할을 수행하여야 한다. 본 연구에서는 이와 같은 문제 인식을 토대로 확률적 사고의 관점에서, 특히 확률적 사고의 발달의 핵심 개념이라 할 수 있는 우연과 무작위성을 중심으로 현재 초등학교 수학에서 다루고 있는 가능성 지도의 보편적인 문제점을 2015 개정 초등학교 수학과 교육과정 문서 및 교과용 도서의 사례를 바탕으로 비판적 문헌 분석을 수행하고자 한다.

연구 방법

본고의 목적은 무작위성, 우연, 확률적 사고 등 수학교육 연구 중에서도 수학 내용 지식의 내적인 논리에 비추어 우리나라 초등학교 수학에서 가능성 지도와 관련한 문제점을 포착하고 그 개선 방안을 탐색하는 데 있다. 그러나 실험, 평가, 관찰, 조사 등과 같은 전형적인 연구 방법으로는 이러한 목적을 달성하기 어려우며, 다음과 같은 상황에서는 문헌 연구 방법으로서 철학적 연구 방법을 사용할 수 있음이 알려져 있다.

관련 문헌을 통해 필요한 자료나 해당 연구와 관련된 이론은 이미 주어져 있되, 그 자료들에 내재된 특정 수학교육 현상들 사이의 관계성에 대한 통찰로부터 시작된 연구의 문제의식과 함께 그 관계성을 기존의 관련 이론을 통해서 드러내기 위하여 이루어지는 연구 방식의 경우는 앞서 거론한 연구 방법들에 의해서는 해당 연구 문제의 답을 구하거나 연구 목적을 이루어내기에 불편하거나 어려운 경우가 있다. 이와 같이 전술한 예로부터 특유의 연구 필요성이나 방법론이 설명될 수 있는 연구 방법을 ‘철학적(philosophical)’이라는 수식어로 나타내는 것을 볼 수 있다(Song et al., 2013, p. 19).

철학적 연구 방법이란 “연구자가 기존 문헌에 대한 숙고를 통하여 서로 다른 관점들을 융합함으로써 이미 연구된 동일 현상이나 행위에 대한 보다 발전된 해석이나 설명을 가능케 해주는 연구 방법”이다(Johnson, 1980, p. 24). 연구자의 사유에 기반을 둔다는 점에서 엄밀한 과학적 형식을 취하는 것은 아니나, 기존의 자료나 정보를 탐색하는 주체가 새로운 사실이나 통찰을 도출하는 과정에서 결과에 다다르기까지의 추론과 재구성, 그리고 논리의 일관성이 정형화된 절차적 방법을 대체하는 것이다. 특히, 그동안 교육과정을 개정한 후에는 그 적절성에 대한 연구자들의 비판적 관점을 담은 연구가 꾸준히 수행되어 왔는데(e..g., Choi & Lee, 2014; Kang, 2013; Park & Kwon, 2012), 이러한 연구들 모두 과학적 진리(眞理)를 탐색하기보다는 연구자의 사유와 그 논리적 정합성을 토대로 일리(一理)의 논점을 도출하기 위한 목적으로 선행연구와 교육과정 및 교과서를 고찰하였다.

본 연구 역시 이와 같은 문제의식을 바탕으로 철학적 연구 방법을 적용하여, 본 연구에서는 우리나라 초등학교 수학과 교육과정에서 가능성 지도에 대해 비판적으로 고찰하고 그 문제점을 제시한다. 이는 “학교수학의 특정한 주제를 가르치기 적절하게 교재와 수업을 조직하는 데 유용한 시사를 얻기 위해 그 주제의 본질을 여러 측면에서 분석하는 교수학적 분석(didactical analysis)”의 일환이기도 하다(Woo et al., 2006, p. 31). 구체적으로 Ⅱ장에서 다룬 우연과 무작위성을 바탕으로 한 확률적 사고의 발달이라는 관점에서 2015 개정 초등학교 수학과 교육과정에서 가능성 지도와 관련한 문서 체제 및 교과용 도서를 분석하고, 선행연구 및 외국의 교육과정과 교과서 사례를 활용하여 우리나라 초등학교 수학에서 가능성 지도의 몇 가지 문제점을 짚어본다. 확률의 지도에서 빈도주의적 접근과 통계와의 관계에 주목하여 확률을 지도할 것을 강조하면서 확률교육을 강화하는 미국, 호주, 뉴질랜드의 교육과정과 비교 분석하였으며, 가능성에 대한 지도가 초등학교 5학년에서 이루어진 이후 중학교 2학년에서 다루어지는 우리나라 교육과정의 특성을 반영하여 가능성에 대한 연속성 있는 지도에 대한 측면에서 문제점을 살펴보고자 분석의 범위를 중학교 교육과정까지 확장하였다.

연구 결과

자료 기반 추론 경험의 결여

확률 개념은 경우의 수의 비로 나타내는 고전주의적 확률, 상대도수의 극한값으로 정의되는 빈도주의적 확률이 있으며, 이는 고등학교 수학과 교육과정에서 각기 수학적 확률, 통계적 확률이라는 명칭으로 다루어진다. 또한, 최근에는 인공지능이 임의 할당을 통해 초깃값을 설정한 뒤 기계학습을 통해 자료를 기반으로 확률을 개선해나가는 베이즈 통계학의 방식이 널리 활용되면서 주관주의적 확률 개념 또한 지금보다는 이른 시기에 다루어질 필요가 있다는 주장이 제기되고 있다(e.g., Jessop, 2010; Hoegh, 2020). 이와 같이 확률 개념은 그 인식론적인 배경에서부터 매우 복잡하기에 초등학교 수준에서 온전히 이해하기에는 분명 어려운 개념이며, 이러한 배경으로 인해 2009 개정 수학과 교육과정에서는 초등학교 수준에서 고전적인 확률 개념에 앞서 실생활에서 경험하는 확률의 기초 개념인 가능성을 다루는 방안을 모색한 것이다(KOFAC, 2015, p. 81).

비록 엄밀한 확률 개념은 매우 복합적인 성격을 띠지만, 가능성에 대한 관념은 Piaget와 Inhelder (1975)나 Fischbein (1975)의 연구에서도 확인할 수 있듯이 매우 어린 나이에도 비형식적인 수준에서 형성된다고 볼 수 있다. 길이나 무게와 같이 셈을 통해 수와 연결지을 수 없는 속성도 시각, 촉각과 같은 감각을 통해 양(量)으로 인식하듯, 인간은 어떤 일이 일어날 가능성 또한 빈번한 것과 드문 것을 구분하여 대소 비교가 가능한 양으로서 직관적으로 인식하는데, 이를 확률 직관이라 한다. 2009 개정 수학과 교육과정에서부터 초등학교에서 확률 대신 가능성을 지도하게 된 이유는, 확률 개념이 인간의 정신 외적으로 정의된 추상적이고 형식적인 개념이 아니라 인간의 내재된 확률 직관으로부터 인지된 가능성이 수학화를 거쳐 추상화된 것으로 볼 수 있기 때문일 것이다. 즉, 형식적인 확률 개념을 직접 도입하기에 앞서 가능성에 대해 인지하고 일정한 수학화 과정을 거쳐 확률을 학습하는 것이, 불확실성, 우연, 승산과 같은 용어에서 드러나는 비결정론적 인식을 모델링하여 가능성을 수량화하는 확률 개념의 본질을 이해하는 데 도움이 될 것이라는 판단이 있었던 것으로 보인다.

그러나 확률적 사고의 발달이 이루어지기 위해서는 모호하고 비형식적인 직관의 영역에서 벗어나 논리와 형식을 갖춘 추론의 영역으로 나아갈 수 있어야 한다. Jones 외 (1997)와 같이 전통적인 관점에서 확률교육을 연구해 온 연구자들은 확률적 사고 수준의 발달을 무작위성의 이해를 바탕으로 한 확률의 수치적 할당으로 바라보았지만, 오늘날에는 자료에 기반을 두어 확률을 구하고 이를 통해 실세계 현상에서 가능성을 예측하는 것이 더 중요하게 다루어진다(Nilsson, 2013). 이에, Callingham 외 (2021)는 호주의 수학과 교육과정에서 확률과 통계 영역의 지도 목표로서 통계적 추론을 강조하였고 그 유형을 크게 기대 속성과 무작위성 기반의 변이 추론(variation with expectation and randomness, VER), 분포와 기대 속성 기반의 변이 추론(variation with distribution and expectation, VDE), 비형식적 추리 기반의 변이 추론(variation with informal inference, VII)으로 분류하면서, 이 중 VER이 바로 확률 개념의 학습을 통해 신장되어야 할 통계적 추론이라 강조한 것이다. 이는 확률교육이 확률 직관에 기반을 둔 가능성 지도만으로 마무리 지어서는 안 되며, 과학적인 추론의 수준으로 나아가도록 일정한 발판을 마련할 필요가 있음을 보여 준다. 특히, 오늘날에는 그 발판으로서 Figure 4와 같이 자료를 이용한 확률 모델의 개선에 주목하고 있다(Pfannkuch et al., 2016).

Figure 4. Framework for probability modeling cycle (Pfannkuch et al., 2016, p. 24).

그러나 현재 2015 개정 수학과 교육과정에서는 초등학교 5학년에서 확률 직관에 의지하여 가능성을 수로 나타낼 수 있다는 정도만 다루고 있고, 중학교 2학년에서 바로 고전주의적 확률과 빈도주의적 확률을 형식적으로 정의하고 있다. 초등학교 가능성 지도는 학생들의 모호한 감각과 경험, 직관에 의존하여 ‘불가능하다’, ‘반반이다’, ‘확실하다’와 같은 언어적 표현을 사용케 한 뒤, 이를 그대로 0, $\frac{1}{2}$, 1에 대응하여 다룬다. 즉, 가능성을 어떤 수로 나타내어야 할지를 판단하는 데 자료에 근거를 두는 경험이 주어지지 않는 것이다. 이와 같이 초등학교 수준에서 가능성에 대한 직관적 인식만으로 학습이 마무리된 상태에서 중학교 2학년 때 형식적인 확률 개념을 바로 접하게 되면, 오히려 초등학교에서 다룬 가능성과 중학교에서 다루는 확률 개념이 더욱 유리되는 상황이 전개될 우려가 있다.

무작위성 지도의 누락

확률 직관에 의존하여 가능성을 인식하고 이를 말이나 수로 나타낼 때는 인식 주체의 경험이 매우 중요하다. 예를 들어, “오늘 학교에 전학생이 올 것이다”와 같은 일이 일어날 가능성은 전학생이 오는 일이 그다지 자주 일어나지 않는다는 경험에 의존하여 매우 낮을 것이라 판단할 수 있다. 그러나 자료에 기반을 둔 확률적 사고가 이루어지려면 이러한 경험에 대한 논리적인 판단이 추가되어야 한다. 이러한 논리적 판단이 이루어지려면 무작위성에 대한 이해가 필요하다.

무작위성 개념의 의미는 역사적으로 다양한 아이디어와 결합하여 발전해왔으나(Ko & Lee, 2010), 통계학에서 무작위성은 “개개의 결과는 불확실하지만 여러 번의 반복 시행에서는 일정한 패턴을 지니는 속성” 정도로 정의할 수 있다(Moore, 1990, p. 98). 이러한 정규적 패턴이 드러날 수 있도록 현실 세계에서 무작위성을 전제하려면 편향(bias)을 유발할 수 있는 외부 영향을 최대한 배제했는지에 대한 맥락적인 판단이 선행되어야 한다. 즉, 동전을 던져 앞면이 나올 가능성을 $\frac{1}{2}$이라 주장하는 배경에는, 단순히 동전의 앞면과 뒷면이라는 경우만이 아니라 동전이 휘어져 있지는 않은지, 밀도가 균등한지 등 편향을 유발하는 맥락적 요소를 따져 보고 무작위성을 전제할 수 있는지에 대한 판단이 선행되어야 한다. 물론, 무작위성의 전제는 편향에 의해 반증가능할 뿐, 연역적으로 입증가능하지는 못하기에 직관에 의존하는 것이 자연스러운 현상이다. 그러나 단순히 직관에 의해서 가능성을 곧바로 판단하는 것보다는 맥락 속에 편향이 없는지를 탐지한 후에 무작위성을 전제하여 가능성을 판단하는 것이 논리적으로 수준이 높은 확률적 사고에 해당한다.

2015 개정 수학과 교육과정에서는 초등학교에서 가능성을 지도하는 데 표본공간을 다루지 않고 바로 중학교에서 확률 개념을 도입한다. 그러나 무작위 시행에서 등확률성을 바탕으로 표본공간을 구성하는 활동 경험이 초등학교 수준에서 이루어지지 않는다면, 이후 중학교에서 이론적이고 선험적인 고전주의적 확률을 온전히 이해하고 현실 상황을 모델링하는 데 확률이 사용되는 원리를 깨닫기 어려울 수 있다. 심지어 현재 우리나라 수학 교과서에서는 Figure 5와 같이 무작위성을 전제하기 어려운 맥락이 부여되어 있음에도 무작위성을 전제하여 해결해야 하는 과제가 제시되어 있다. ○× 문제를 푸는 상황이기 때문에 결과적으로 나타나는 경우는 지혜가 문제를 맞추는 경우와 맞추지 못하는 경우, 이렇게 2가지이며 원소가 2개인 표본공간을 구성할 수 있다. 여기에서 각 원소가 나타날 가능성은 지혜의 실력에 의존하기 때문에, 동전을 던지는 상황처럼 문제를 맞출 가능성을 $\frac{1}{2}$이라 주장할 수 없다. 지혜의 실력에 비추어 문제의 난도가 낮다면 문제를 맞출 가능성은 $\frac{1}{2}$보다 더 크다고 보는 것이 타당할 것이다. 그러나 일반적으로 문제를 풀 때 O, X를 답하는 시행은 무작위로 이루어지지 않음에도 불구하고, Figure 5 문항의 답으로 “반반이다”, “$\frac{1}{2}$”을 제시하고 있는 것이다. 이는 우리나라의 초등학교 수학에서 가능성을 지도할 때 무작위성, 등확률성이 제대로 고려되지 않고 있음을 보여준다.

Figure 5. A task of chance with randomness in the Korean mathematics textbook (MOE, 2019b, p. 91).

경우의 수의 인위적 배제로 인한 모순

2009 개정 수학과 교육과정에서는 교수 〮 학습 상의 유의점으로 “사건이 일어날 가능성은 0, $\frac{1}{4}$, $\frac{1}{2}$, $\frac{3}{4}$, 1 정도로 표현할 수 있게 한다”를 제시하고 있다(MOEST, 2011, p. 27). 그러나 2015 개정 수학과 교육과정의 교수 〮 학습 방법 및 유의사항에서는 $\frac{1}{4}$, $\frac{3}{4}$가 삭제되고 “가능성을 수로 표현할 때 0, $\frac{1}{2}$, 1 등 직관적으로 파악되는 경우를 다룬다”고 제시되어 있는데(MOE, 2015, p. 28), 교육과정 연구진은 이와 같은 개정을 학생들이 가능성을 수로 나타낼 때 경우의 수를 고려해야 하는 경우를 배제하기 위한 조치라고 설명하고 있다(KOFAC, 2015, p. 81). 또한, ‘직관적으로 파악되는 경우’라는 명시적 표현을 통해, 초등학교 수준에서 가능성을 수로 나타내는 것은 어디까지나 확률 직관에만 의존하는 것으로 한정지었음을 드러내고 있다. 현재 우리나라 초등학교 수학 교과서에서는 가능성을 수로 나타내는 법을 지도하기 위해 회전판(spinner)을 활용하고 있다. 한편으로 영역의 상대적인 비중을 비율로 나타낼 수 있다는 점에서, 다른 한편으로 회전판을 돌리는 시행의 무작위성을 직관적으로 인식할 수 있다는 점에서, 회전판은 가능성을 수로 나타내는 방법을 지도하는 데 매우 유용한 모델이다. 그러나 회전판의 영역 또한 표본공간에 해당하지만, 우리나라 수학 교과서에서는 이를 구체적으로 드러내어 지도하기보다는 0, $\frac{1}{2}$, 1의 경우를 각기 “불가능하다”, “반반이다”, “확실하다”와 같은 정형화된 언어적 표현에 대응하는 수준에서만 마무리짓고 있다.

정작 우리나라 초등학교 수학 교과서에서 가능성을 수로 나타내는 과제의 대부분은 동전과 주사위에 의존하고 있다. 실제로 동전과 주사위를 던지는 행위는 학생들이 쉽게 무작위 시행으로 인식하며 매우 간단한 표본공간을 갖추고 있어 가능성에 대한 직관적 인식을 형식적인 확률 개념으로 연결하는 데 활용될 수 있는 가장 기본적인 소재이다. 그러나 동전과 주사위는 KOFAC (2015)이 지향하는 바처럼 경우의 수를 배제할 수는 없는 소재이다. 학생들이 동전을 던져서 앞면이 나올 가능성을 $\frac{1}{2}$이라 판단하는 이유는 {앞면, 뒷면}이라는 크기 2의 표본공간을 자연스럽게 구성할 수 있기 때문인데, 이는 경우의 수를 배제한 판단으로 보기 어렵다. 주사위는 경우의 수를 배제하고 직관적인 판단에만 의존하도록 한다는 의도에 더욱 모순되는 소재이다. Figure. 6의 첫 번째 문항에서 주사위의 눈의 수가 짝수일 가능성을 판단하는 근거는 세상에 홀수와 짝수가 반반씩 존재한다는 직관이 아니라, 6개의 표본공간 원소 중 짝수에 해당하는 원소가 3개라는 사실이다. 즉, 주사위의 눈의 수가 짝수일 가능성은 직관적으로 “반반이다”라고 인식하여 $\frac{1}{2}$로 변환되는 것이 아니라, 경우의 수를 통해 3/6이 되는 것이다. 이 외에도 Figure. 6의 두 번째, 세 번째 문항과 같이 카드나 구슬을 뽑는 시행이 교과서에 제시되는데 이는 모두 표본공간을 구성하여 경우의 수를 고려해야만 가능성을 수로 나타낼 수 있는 상황이다.

Figure 6. Tasks of quantifying chances in the Korean mathematics textbooks (MOE, 2019a, pp. 139, 143; MOE, 2019b, p. 91).

특정 학년에 편중된 구성

Piaget와 Inhelder (1975)에 따르면 일반적으로 아동은 7~8세 시기에 우연과 필연을 구분하고 직관적 수준에서 우연을 인식함으로써 가능성 관념을 발달시킨다고 알려져 있다. Fischbein (1975)은 그보다 이른 시기인 학령기 이전에도 확실한, 불가능한, 가능한 사건을 구별하고 간단한 사건에 대해서는 우연 속성과 가능성을 파악할 수 있다고 주장하였다. 즉, 아동의 확률적 사고는 매우 어렸을 때부터 비형식적인 수준에서 시작한다는 것을 알 수 있으며, 이에 형식적인 확률 개념을 지도하기에 앞서 초등학교 수준에서 직관과 경험을 토대로 가능성을 지도하는 것은 저학년 수준에서 이루어질 수 있음을 알 수 있다. 실제로 미국수학교사협의회(National Council of Teacher of Mathematics)에서 발행한 『학교수학을 위한 원리와 규준』에서도 내용 규준 중 하나인 ‘자료 분석과 확률’을 통해, 유치원부터 2학년까지의 확률 지도에 대해 다음과 같이 기술한 바 있다(NCTM, 2000).

확률의 기본 개념 이해 및 적용

Pre-K에서 2학년 수준에서의 확률 경험은 비형식적이어야 하며, 일어날 것 같은, 일어날 것 같지 않은 등의 단어를 사용하여 사건의 가능성에 대해 답하는 형식을 취해야 한다. 어린 학생들은 불가능한 사건에 대해 사고하는 것을 즐기며, 읽고 있는 책에서 불가능한 사건들을 마주치기도 한다. 일어날 것 같은 사건과 일어날 것 같지 않은 사건에 대한 질문은 학생들의 경험으로부터 도출되어야 하며, 답은 학교가 속해 있는 공동체와 그 위치에 의존해야 한다. 겨울이라고 하더라도, “내일 눈이 올까?”와 같은 질문은 지역에 따라 매우 다른 답이 나올 것이다.

교사는 회전판이나 주사위로 하는 비형식적인 활동을 통해 확률을 도입해야 하며, 이를 통해 수 규준을 중심으로 해서 다른 규준에서의 개념을 강화해야 한다. 예를 들어, 학생들이 두 개의 주사위를 던지고 나온 눈의 수를 더하는 활동을 반복할 때, 학생들은 결과를 이해할 것이다. 학생들은 두 눈의 합이 1이 나오는 경우는 불가능하며, 두 눈의 합이 2나 12인 경우는 매우 드물고, 두 눈의 합이 6, 7, 8인 경우는 흔하다는 것을 인식할 것이다. 학생들은 토론을 통해서 관찰 결과가 두 개의 주사위로부터 특별한 합을 얻는 방식의 개수와 관련됨을 인식할 것이다. 그러나 정확한 확률 계산은 더 높은 학년에서 이루어져야 한다(NCTM, 2000, pp. 116-117).

미국뿐만 아니라 호주와 뉴질랜드에서도 가능성 지도는 Table 2와 같이 초등학교 저학년에서부터 이루어진다. 예컨대, Figure 7의 왼쪽은 호주의 초등학교 1학년 수학 교과서에 제시된 가능성 지도 내용이다. 삽화를 통해 제시된 각 사건이 일어날 가능 여부를 판단하고, 일어날 법한 사건과 일어나지 않을 법한 사건을 일상 언어로 표현하는 과제가 제시되어 있다. 우리나라는 이와 비슷한 과제가 Figure 7의 오른쪽과 같이 초등학교 5학년 수학 교과서에 제시되어 있다. 즉, 가능성을 직관적으로 인지하여 일상 언어로 표현하는 활동은 미국, 호주, 뉴질랜드에서 1~2학년 때 지도하고 있는 데 반해, 우리나라에서는 5학년에서 지도하고 있는 것이다.

Figure 7. Tasks of representing chances in the Austalian mathematics textbooks for 1st grades (Weeks, 2012, p. 113) and the Korean mathematics textbooks for 5th grades (MOE, 2019a, p. 133).

이는 Table 2에서 확인할 수 있듯이 우리나라에서는 초등학교에서 가능성을 지도하는 시기가 5학년으로 한정되어 있기 때문이다. 미국, 호주, 뉴질랜드 모두 1~2학년 수준에서 가능성을 나타내는 언어적 표현을 바탕으로 필연과 우연을 구분하는 활동으로부터 가능성 지도를 시작한다. 3~4학년 수준에서는 상황에 대한 직관적 파악이나 실험을 통한 자료 관찰을 바탕으로 우연변이성을 경험케 하는 내용이 제시되어 있으며, 5~6학년 수준에서는 등확률성에 대한 탐구와 함께 가능성을 수로 나타내는 활동을 다루고 있다. 7학년 이후에는 사건의 독립, 종속까지 아우르면서 가능성 관념에 수학적 형식을 부여하고 확률의 성질을 탐구하는 활동을 나아가고 있다. 반면, 우리나라는 가능성을 말과 수로 표현하고 비교하는 낮은 수준의 활동만 5학년에서 다루고 있으며, 중학교 2학년에서는 바로 추상적인 확률 개념과 성질의 지도가 이루어져 미국, 호주, 뉴질랜드와 비교했을 때 내용과 시기, 양 측면에서의 간극이 상당하다는 점을 확인할 수 있다.

Table 2. Chance and probability in mathematics curriculum for 1st ~ 8thg rades in Korea, US, Australia, and New Zealand.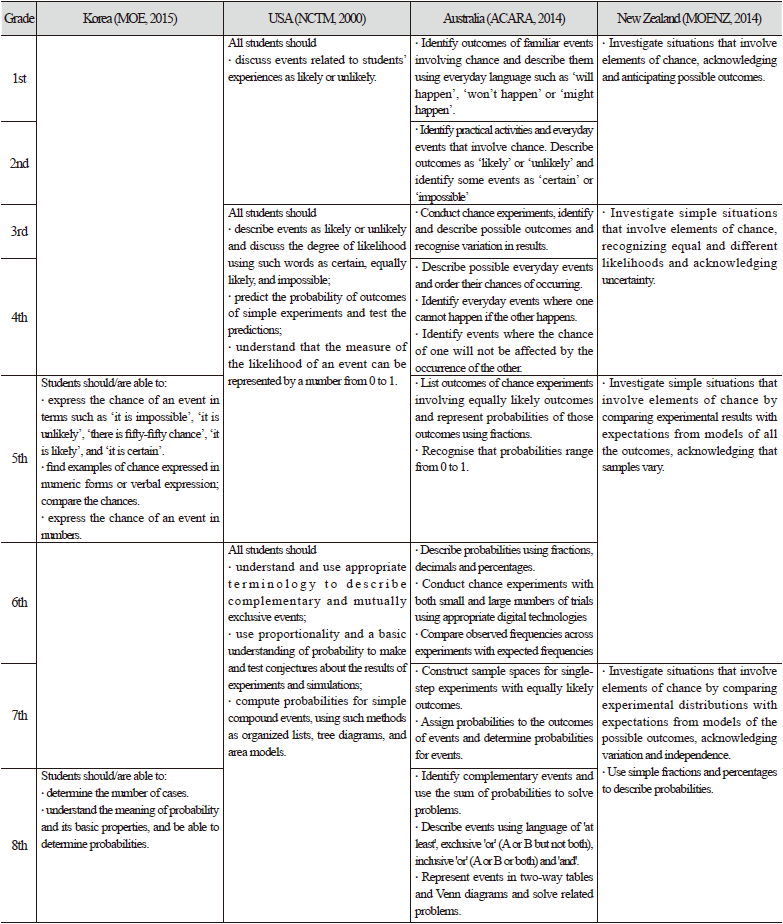

2007 개정 수학과 교육과정까지는 이 시기에 경우의 수를 이용한 고전주의적 확률 개념을 직접적으로 지도하였다. 그러나 2009 개정 수학과 교육과정에서부터는 확률 대신 가능성이라는 용어를 사용하여 형식적인 확률을 도입하기에 앞서 직관에 의존하는 비형식적인 확률적 사고에 주안점을 두기 시작하였다. Chang (2013)은 이와 같은 변화에 따라 가능성을 처음 지도하는 시기를 이전보다 낮은 초등학교 3~4학년군으로 제안하였으나 실제로 반영되지는 못하였다. 이는 우리나라의 수학 교과서 체제가 학기별 6단원으로 고정되어 있고 단원별로 10차시 내외를 균형있게 할당해야 한다는 관습으로 인해, 전 학년에 걸쳐 가능성을 지도할 수 있는 나선형 교육과정의 여지가 존재하지 않기 때문인 것으로 보인다. 이로 인해, 우리나라의 수학과 교육과정에서 확률교육은 초등학교 5학년 때 처음으로 외국에 비해 매우 낮은 수준의 가능성 지도가 이루어지고, 다시 형식적인 확률 개념이 지도되는 중학교 2학년에 이르기까지 가능성과 확률에 대한 내용이 전혀 언급되지 않는 분절적인 형태를 띠고 있다.

논의 및 결론

최근 우리나라 초등학교 수학과 교육과정에서는 확률의 지도와 관련하여 큰 변화가 있어 왔다. 초등학교에서 확률의 정의 대신 확률을 위한 직관적 개념으로서 ‘가능성’을 지도하고, 초등학교 수학의 ‘확률과 통계’라는 영역명이 ‘자료와 가능성’으로 변경되었다. 우연과 무작위성이라는 아이디어를 다루는 확률 개념이 가능성을 수량화하는 경험을 통해 발달해 왔다는 배경을 반영한 이러한 변화는 교육과정이 구현되는 교과서 활동에도 적절히 반영되어야 의미가 있을 것이다. 이에 본 연구에서는 가능성 지도의 목표가 확률적 사고의 발달이라는 점을 고려하였을 때, 우리나라 초등학교 수학에서 가능성 지도와 관련한 문제점은 무엇인지 확인하고, 확인된 문제점을 해결하기 위한 가능성 지도의 개선 방안은 무엇인지 분석하였다. 이를 위해 우연과 무작위성에 대해 살펴보았으며, 교수학적 분석을 통해 우리나라 초등학교 수학과 교육과정에서 가능성 지도가 우연과 무작위성의 개념 지도와 관련하여 어떻게 지도되고 있는지 비판적으로 고찰하였다. 연구 결과, 우리나라 초등학교 수학에서 가능성 지도의 문제점으로 (1) 자료 기반 추론 경험의 결여, (2) 무작위성 지도의 누락, (3) 경우의 수의 인위적 배제로 인한 모순, (4) 특정 학년에 편중된 구성을 확인하였다. 이 장에서는 위와 같은 문제점의 개선 방안에 대해 논의한다. 확률 지도의 개선을 위해 크게 확률 실험의 지도와 표본공간의 지도를 제시할 수 있으며, 특정 학년에 편중된 구성을 위해 자료 영역의 내용 조절과 절충을 지도할 수 있다. 먼저 확률 실험의 지도와 표본공간의 지도에 대해 논의하면 다음과 같다.

Figure8. Distribution of the number of times a coin comes down tail when tossed 6 times (Ko & Hwang, 2020, p. 952).

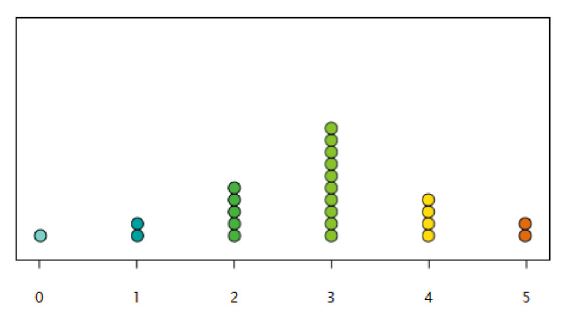
첫째, 확률 실험의 지도를 통해 자료 기반 추론 경험의 결여의 보완을 고려해볼 수 있다. 1개의 동전을 던질 때 앞면과 뒷면이 나올 확률은 $\frac{1}{2}$로 서로 같다. 그래서 1개의 동전을 6번 연속해서 던질 경우 앞면과 뒷면이 각각 3회씩 나타날 것이라 예상해볼 수 있다. 그러나 하나의 동전을 5번 연속해서 던진 결과가 ‘앞, 뒤, 앞, 앞, 뒤’이라 해서 다음 시행에서 반드시 뒷면이 나타난다고 확신하지 못한다. 뒷면이 나타난다면 예상했던 $\frac{1}{2}$과 일치하지만 앞면이 나타난다면 예상과는 다른 결과를 얻게 되는 것이다. 앞면이 나타날지 뒷면이 나타날지는 우연(chance)에 의해 결정된다. 그러나 1개의 동전을 6회 던지는 시행을 여러 번 실시한 후 뒷면이 나타나는 횟수의 분포를 조사하면 Figure 8과 같이 3회를 중심으로 분포됨을 확인할 수 있다. 이러한 현상은 6회를 던지는 시행의 횟수가 증가할수록 더 분명해진다. 이때 분포는 고전주의적 확률을 반영하는 신호(signal) 부분, 즉 확률 $\frac{1}{2}$에 의해 예상 가능해지는 3과 우연(chance)에 의해 만들어지는 소음(noise) 부분으로 구성된다. Konold와 Pollatsek (2002)은 확률적 사고에서 인과적(causal) 변이와 무작위(random) 변이를 구분하는 능력이 중요하다고 하면서 이를 소음(noise) 속에서 신호(signal)를 감지해내는 것으로 비유하였다. 확률 실험의 결과를 분포로 나타내고 분포에 대한 탐구를 통해 우연과 무작위성 개념에 대한 이해를 개발함으로써 소음 속에서 신호를 감지해내는 감각이 길러질 수 있다. 이와 같이 확률 실험에 대한 분포 탐구 활동이 유의미하게 이루어지기 위해서는, 가능성을 직관 수준에서만 다루기보다는 자료를 바탕으로 추론하고 가능성에 근거하여 적절한 판단을 하는 경험을 제공할 수 있도록 교육과정의 성취기준을 보강할 필요가 있어 보인다. 그리고 이를 교수‧학습 차원에서 구현하기 위해서는 공학 도구의 활용이 절실하므로, 초등학교 수준에서 공학도구의 활용에 대한 연구가 함께 이루어질 필요가 있다.

둘째, 표본공간의 지도를 통해 무작위성의 이해를 독려할 수 있다. 무작위성을 이해하고 이를 바탕으로 추론이 이루어지도록 표본공간의 지도를 고려해볼 수 있다. 표본공간은 시행을 통해 나타날 수 있는 모든 사상을 원소로 하는 집합을 의미하지만, 이때의 시행이 무작위 시행(random experiment)이어야 비로소 각 사상의 등확률성을 전제할 수 있게 되어 가능성을 수로 나타내는 근거를 제공한다. 즉, 학생이 표본공간을 어떻게 구성하는지에 따라 무작위성을 이해하고 있는지를 판단할 수 있으며, 따라서 어떤 일이 일어날 가능성을 판단하기 위해 표본공간을 구성하는 활동은 무작위성을 전제할 수 있는가에 대한 합리적인 추론 경험을 제공한다. 이에 호주의 초등학교 수학 교과서에서는 Figure 9와 같이 3학년 때 무작위 시행으로부터 등확률성을 판단할 수 있는 사례를 제시하고 있으며, 6학년 때는 표본공간을 직접적으로 지도하고 있다.

Figure9. Tasks of randomness and sample spaces in the Australian mathematics textbooks (Weeks, 2011, p. 121; Carr, 2011, p. 128).

우리나라의 경우 초등학교 수학과 교육과정에 ‘표본공간’이라는 용어를 들여오는 것에 대해서는 신중할 필요가 있다. 그러나 KOFAC (2020)이 표본공간 개념을 초등학교 수학에서 지도할 수 있는 방안을 모색할 필요가 있음을 제안한 바 있다(p. 76). ‘표본공간’이라는 용어를 도입하지 않더라도 ‘하나의 동전(또는 주사위)을 던졌을 때 나올 수 있는 것에는 어떠한 것이 있는지 모두 나열해보시오’와 같이 직관적이고 비형식적으로 표본공간을 구성해 보도록 하는 것은 하나의 대안이 될 수 있을 것이다. 또한, 현재 2015 개정 수학과 교육과정에서 가능성을 수로 나타내는 범위를 0, $\frac{1}{2}$, 1로 제한하고 있는데, 적어도 제비뽑기나 주사위와 같은 맥락을 활용하기 위해서는 $\frac{1}{3}$, $\frac{1}{4}$, $\frac{1}{6}$정도까지 허용할 필요가 있다. 이때의 $\frac{1}{6}$은 가능성이 각 6가지 경우에 의해 ‘등분’된 것으로 바라보는 것이기 때문에 ‘6가지 경우의 수 중 한 가지 경우의 수’와 같은 조합론적인 접근과는 차이가 있다. 또한, 표본공간에 대한 탐구는 확률 실험에서 시행횟수가 늘어남에 따라 분포의 향상이 어떻게 변화하는지, 그 변화 과정에서 무엇이 소음이고 무엇이 신호인지를 판단하기 위해 전제되어야 할 필요가 있다.

셋째, 자료 영역의 학습 내용 조절을 통해 특정 학년으로의 가능성 영역의 학습 내용의 편중을 완화할 수 있다. ‘2-2-5. 표와 그래프, 3-2-6. 자료의 정리, 4-1-5. 막대그래프, 4-2-5. 꺾은선그래프, 6-1-5. 여러 가지 그래프’단원에서는 자료 영역에 대한 지도만 이루어지고 있다. 학습 내용의 조절이 가능한 단원에서 가능성 영역의 학습 내용을 2~3차시 정도 지도하는 방법을 모색한다면 가능성 영역의 학습 내용이 특정 학년에 편중되는 것을 완화할 수 있으며, 또한 내실 있는 지도가 이루어질 수 있을 것이다. 또한 초등학교 5학년에서 이루어진 이후 중학교 2학년에서 다루어지는 지금과 같은 단절적인 전개를 피함으로써 좀 더 연속적이고 체계적인 지도가 이루어져 학생들이 초등학교와 중학교 과정에서 좀 더 견고한 확률적 사고를 다질 수 있을 것이다. Lee 외 (2021)는 학교수학에서 확률과 통계 영역이 이론 대신 자료에 기반을 두는 방향으로 수학과 교육과정이 재구조화될 필요성이 있음을 제시한 바 있다. 확률 현상에 대한 이해를 토대로 초등학생들의 확률적 사고를 발달시켜 중·고등학교 수준에서 이루어지는 형식적인 수준의 확률 개념 학습으로 간극 없이 연결하려면, 형이상학적 관념인 우연과 무작위성을 초등학생들이 직접 인지할 수 있는 자료 기반의 시각화 표현이 유용하게 활용될 필요가 있다.

지금까지 우리나라 초등학교 수학과 교육과정에서 가능성 지도에 대한 문제점의 방안으로 자료 영역의 내용 조절과 절충을 제안하면서 또한 확률 실험의 지도와 표본공간의 지도도 함께 제안하였다. 마지막으로 본 연구에서는 가능성 개념이 우연과 무작위성의 개념과 관련하여 지도되기 위해 확률 실험과 표본공간의 지도는 초등학교와 중학교 교육과정의 연속선상에서 고려해볼 필요가 있음을 주장하고자 한다. 확률 실험과 표본공간을 지도하기 위해 어떤 것이 학습 요소로 추출되어야 하는지, 추출된 학습 요소의 위계는 어떻게 설정하고 어느 학년에서 지도하는 것이 적절한지에 대한 포괄적인 논의가 이루어질 필요가 있다.

Acknowledgements

이 연구는 2021년 전주교육대학교 국립대학육성사업의 연구비 지원으로 수행하였음

This work was supported by the 2021 National University Development Project in Jeonju National University of Education

Footnote

1 호주와 뉴질랜드는 다른 나라에 비해 확률과 통계 영역에 대한 연구가 활발히 이루어진다는 평가를 받기에 확률과 통계 영역의 개선을 위한 선행연구에서 자주 인용되는 국가이다(KOFAC, 2014).

2 뉴질랜드의 학제는 총 13학년으로 구성되어 있으나 교육과정 문서는 8개의 수준으로 제시되어 있다. 학년과 수준이 명확하게 대응되는 것은 아니나 뉴질랜드 국가 규준(National Standards)에 따르면 한 수준의 내용이 대략 2년 정도에 걸쳐 지도된다고 볼 수 있기에(Kim, 2019, p. 628), Table 2에서는 1~2학년에 1수준 내용을, 3~4학년에 2수준 내용을, 5~6학년에 3수준 내용을, 7~8학년에 4수준 내용을 제시하였다.

3 2015 개정 수학과 교육과정 문서는 학년군 체제를 따르고 있어 가능성에 해당하는 내용은 5~6학년군으로 분류되어 있다. 그러나 교과서에서는 5학년 2학기에서만 가능성을 다루고 있으며, 실제 초등학교 6년 과정 중 가능성 지도가 이루어지는 시간은 약 3~4차시에 불과하다. 이에 Table 2에서는 가능성에 대한 성취기준을 5~6학년이 아닌 5학년에만 해당하는 것으로 분류하였으며, 같은 이유로 확률에 대한 성취기준 역시 교과서를 기준으로 하여 8학년(중학교 2학년)에만 해당하는 것으로 분류하였다.