Exploring fraction knowledge of the stage 3 students in proportion problem solving

서론

우리는 종종 길이, 경과 시간, 질량 등 무언가의 크기를 알기 위해 그리고 그것들을 비교하기 위해 측정 단위를 생각하게 된다. 수를 사용하여 하나의 크기를 설명할 수 있다는 생각으로부터 어떤 그룹 안에 몇 개의 항목이 있는지 찾고, ‘하나’의 항목을 추상화, 일반화로 생성의 과정을 거치는 것을 von Glasersfeld는 ‘단위화(unitizing)’ 조작으로 보았다(as cited in Ulrich, 2015). 이후로 단위화는 많은 수의 항목들을 동일한 크기로 그룹화하거나 재그룹화하는 방식으로 사용되며, 항목에 대한 추상화, 일반화로부터 그룹화 혹은 재그룹화를 통해 구성된 단위는 여러 수준의 체계(hierarchies) 안에서 작동하게 된다(Ulrich, 2015). Ulrich는 Steffe (2010)의 수 계열(INS, TNS, ENS, GNS)과 Hackenberg와 Tillema (2009)의 곱셈적 개념(MC1, MC2, MC3)에 대한 단위 구조의 체계가 학생의 수학적 활동에서 발달의 중요한 이정표로서 단위 조정의 단계를 나타낸다고 보고, 이를 통해 두 단위 구조의 체계 간에 일대일 대응 관계가 있음을 설명하였다(Ulrich, 2016). 그리고 Norton 외 (2015)는 학생들이 동화(assimilate)시킬 수 있는 단위의 수에 따라 단계적으로 결정되는 학생들의 단위 조정의 능력을 특징지어 세 단계로 제시하였다. 즉, 단위를 생성하는 문제 상황에서 학생들에게 나타나는 활동적 의미로의 단위 조정은 단위의 구성과 단위 조정의 단계를 통해 학생들의 현재 수학적 사고를 특성화할 수 있는 도구가 된다(Norton & Boyce, 2015; Ulrich, 2016).

따라서 자연수 맥락에서의 수세기 스킴으로부터 단위의 구성과 단위 조정이 그동안 관련 없어 보였던 여러 수학 영역에 대한 관련성에 주목하는 계기가 되었다. 예를 들어 학생의 자연수의 곱셈과 나눗셈 문제 해결뿐만 아니라, 분수(Hackenberg & Tillema, 2009; Lee, 2019; Norton & Boyce, 2013; Steffe & Olive, 2010), 정수의 덧셈적 개념 구성(Ulrich, 2012), 비례 추론(Lee & Shin, 2020; Shin et al., 2020), 내포량(Liss Ⅱ, 2019; Steffe et al., 2014), 대수적 추론(Hackenberg, 2013; Hackenberg amp;& Lee, 2015) 등 수학의 많은 영역에서 단위 조정의 중요성이 대두되고 있다.

특히 학생들의 분수 지식의 구성과 관련해서는 자연수 맥락에서의 단위 조작 방식과 분수에서의 단위 조작 방식 사이의 강한 연관성을 발견하며 분수 지식에서의 단위 조정 역할을 강조하였고(Hackenberg, 2010; Hackenberg & Tillema, 2009; Olive & Steffe, 2002), 이를 바탕으로 단위 조정 단계를 고려하여 수학 교과서에서의 분수 도입에 대한 방향성을 제시하기도 하였다(Lee, 2019).

분수뿐만 아니라 비례 추론과 관련해서도 학생들의 단위 조정 단계 혹은 수준에 따라 비례 문제 해결 과정에서의 결과적 차이를 나타내며 단위 조정 수준의 향상과 비례 추론의 발달 사이에 관련성을 시사하였다(Lee & Shin, 2020; Shin et al., 2020). 결국 단위 조정은 분수 지식의 구성과 비례 문제 해결에서 중요한 렌즈로 작용하여 학교 수학에서 학생들의 문제 해결 과정을 설명하기 위한 도구로 강조되고 있다.

한편 비례 추론은 비, 비율과 비례 개념을 중심으로 하여 ‘수와 연산’ 영역에서 분수와 소수, 곱셈과 나눗셈으로부터 도형의 닮음 등과 같이 수학의 많은 부분과 관련되어 있어(Lamon, 2007; Lobato et al., 2010), Lesh 외 (1988)에 의하면 고등 수학의 초석이자 초등 수학의 반석이라고 언급한 바 있으나, 다른 한편으론 학생들에게 많은 어려움을 주고 있는 수학적 추론 영역 중의 하나이기도 하다(Kwon et al., 2007; Lobato et al., 2012; Nabors, 2003). 인지 주체가 자신이 경험한 세계와의 상호작용 과정에서 스킴과 조작을 작동시키는 것을 ‘추론’으로 본다면(Hackenberg & Lee, 2015), 비례 추론은 비례 관계를 이해하고 관련 문제를 해결하는 과정에서 두 양 사이의 관계로부터 변하지 않는 곱셈적 관계를 구성하며 정신적으로 여러 정보를 저장하고 처리하는 능력을 포함하는 수학적 추론의 한 형태이다(Behr et al., 1993). 따라서 비례 추론은 비, 비율과 비례 개념을 포함하여 학생들이 습득해야 하는 다수의 이해관계와 관련된 복잡한 주제이다(Carney et al., 2016). 이러한 비례 추론의 다면적 성격을 감안해 볼 때 학생 스스로가 비례 개념을 수학의 다른 영역에 유창하게 적용시키지 못하는 것도 놀라운 일은 아니다(Carney et al., 2016). 비례 개념으로부터 학생들이 가지게 되는 어려움은 학생들의 생각을 이해하는 것에서부터 연구가 시작되어야 한다는 방향성을 가져왔다(Lamon, 2007). 즉, 학생들의 비례 개념에 대한 구성과 비례 문제 해결 과정에 구체적인 도움을 주기 위해서는 학생의 입장에서 정신적 조작을 통해 양을 구성해 나아가는 과정에 대한 이해가 필요하다. 이러한 방향에서 양에 대한 추론 즉, 양적 추론에 대한 연구가 대두되고 있다(Thompson, 1994). 인지 주체가 ‘단위화’ 조작을 통해 구성한 양인 ‘단위’로부터 양적 조작의 한 형태로서 단위 조정을 본다면, 단위 조정 관점에서 학생들의 비례 문제 해결 과정을 분석하는 것은 학생들이 어떠한 방식으로 조작 활동을 수행해나가는지 구체화시킬 수 있다. 이와 관련하여 단위 조정 이론을 바탕으로 Nabors (2003)는 학생들이 분수 문제를 해결 과정에서 사용할 수 있는 조작 방식이 비례 문제 해결 과정에서 사용되는 조작 방식에 기초를 형성한다고 보았다. 그러나 비 개념과 관련된 문제를 해결하는데 단위 조정 3단계 수준이 필요하다는 것을 제외하고는 구체적으로 무슨 조작이 그러한 문제 해결을 가능하게 하는지에 대한 분석이 부족하였다. 이에 Lee와 Shin (2020), Shin 외(2020)는 ‘구체적 조작’에 초점을 두어 학생들 간의 비례 문제 해결 과정에서 나타난 단위 조정 활동과 조작 방식을 분석하여 학생의 비 개념에 대한 양적 구조가 단위 조정 단계와 어떻게 관련되는지, 또 같은 수준의 단위 구조를 조정하여도 ‘활동 이전’과 ‘활동 중’이라는 차이를 통해 학생의 비례 문제 해결 과정에서 어떠한 차이를 보이는지 살펴보았다.

앞선 선행 연구들이 단위 조정 2단계와 3단계, 혹은 ‘활동 이전’과 ‘활동 중’에서 단위 조정 수준(혹은 단계)의 차이에 따라 비례 문제 해결 과정에서의 그 결과적 차이에 초점을 두었다면, 본 연구는 같은 단위 조정 수준(혹은 단계)에 있는 학생들 간의 문제 해결 과정에서도 서로 다른 결과가 나올 수 있고, 학생들이 문제 해결 과정에서 같은 전략을 사용하여 같은 결과가 나왔다 하더라도 그 사고 과정은 조작적 관점에서 다를 수 있다고 본다. 따라서 활동을 통해 보여지는 관찰 가능한 학생들의 문제 해결 과정에 초점을 두고 학생들이 다루는 양들 사이 관계로부터 어떠한 조작 활동이 비례 문제 해결 과정에서 어떠한 역할에 기여하는지 분수 맥락에서의 조작 활동과 관련하여 비례 문제 상황에 대한 양적 조작 방식을 분석하고자 한다.

이를 위해 분수 맥락에서는 ‘활동을 통해(in activity)’ 3수준 단위 조정이 가능하며, 비례 문제 해결 과정에서 서로 다른 양적 조작의 방식으로 접근했던 두 명의 중학교 1학년 학생에 초점을 두었다. 그리고 두 학생에 대한 분수 맥락에서의 분할 조작과 단위 조정 활동을 상세히 분석함으로써 ‘활동을 통해’ 같은 3수준 단위를 조정하는 방식들 사이에의 공통점과 식별 가능한 차이가 있는지로부터 두 학생의 비례 문제를 해결하기 위해 수행하는 조작 방식에 주목하여 분수 맥락에서의 단위 조정 방식이 어떻게 관련되는지를 살펴보고자 한다. 이를 통해 단위 조정 3단계 학생들이 비례 문제 상황에서 어떠한 조작 활동으로 문제를 해결해 나아가는지 설명적 가설을 제시할 것이다. 이에 따른 연구 문제는 다음과 같다.

첫째, 단위 조정 수준이 같은 두 학생의 분수 맥락에서의 단위 조정 활동과 조작은 어떠한가?

둘째, 단위 조정 수준이 같은 두 학생의 비례 문제 해결에서 나타나는 분수 지식은 어떠한가?

이론적 배경

양적 조작으로서의 단위 조정

본 연구는 양적 추론을 바탕으로 하여 단위 조정을 양적 조작의 한 형태로 보고 있다. 따라서 양적 추론에서의 양적 조작에 대한 간략한 소개와 양적 조작으로서의 단위 조정에 대한 관점을 살펴보고자 한다.

‘양’은 수치적 계산에 초점을 둔 산술적인 대상으로만 문제 상황에서 제시되는 것은 아니며, 학생 스스로 문제 상황으로부터 양에 대한 속성을 인식하고 구성하여 산출해 낼 수 있는 개념이다(Smith & Thompson, 2007). 따라서 학생들은 자신만의 경험을 바탕으로 양을 인식하게 되고, 양들 사이의 관계를 구성해 나가며 양을 추론한다. 양적 추론(quantitative reasoning)은 대상과 대상의 속성을 개념화하여 측정 단위를 인식하고 단위들 사이의 관계를 통해 양적 구조를 만들어 가는 과정이다(Thompson, 2011). Thompson (1994)에 의하면 양적 조작은 인식의 주체가 이미 인지하고 있는 양들 사이의 관계로부터 하나의 새로운 양을 구성해 가는 정신적인 조작이며, “인지 주체가 행동을 내면화(internalization)하고 정신적 조작을 할 때, 이러한 조작은 상황을 표상적으로 이해하도록 하고 상황 자체에 나타나지 않는 수치적 관계에 대한 추론을 이끌어낼 수 있다”(p. 186)고 보았다. 한편, Steffe (2014)는 Thompson이 제시한 ‘양’ 그 자체를 대상에 부여된 개념, 그 개념이 가진 성질, 성질에 대한 측정 단위로 구성되는 하나의 스킴¹으로 보고, 이러한 과정에서 ‘단위’ 개념을 강조하였다. 인식의 주체는 양에 대한 조작을 통해 새로운 양을 구성해 가는 과정에서 다양한 측정 스킴을 구성하게 되는데, ‘단위’는 ‘양’이라는 측정 스킴의 분석을 위한 필수적인 요소가 된다. 따라서 단위, 단위화 조작, 단위 조정 활동을 통해 체계를 구성하며 측정 스킴을 다시 재조직하는 방향으로 나아간다. 이때 단위 조정은 합성 단위(composite units)를 포함하여 단위를 생성하고 그 단위에 포함되거나 구성되는 또 다른 단위와의 관련성을 계속해서 유지해 나아갈 수 있는 능력을 말한다(Steffe, 1992; Norton & Boyce, 2015).

단위 조정은 학생들이 단위를 조정하고 동화할 수 있는 ‘단위 수준(levels of units)의 수’와 활동을 통하여 ‘생성(produce)할 수 있는 수준의 수’로 정의되는 조작의 범주로 나타나며, 단위와 수준은 상황 자체라기보다는 상황이 해석되는 방식에 의해서 특징 지워진다(Norton & Boyce, 2015). Norton과 Boyce는 학생들이 n수준(n은 1, 2, 또는 3)의 단위를 가지고 상황을 해석하는 것으로 상황 안에서 n수준의 단위를 구별할 수 있다고 보았고, n수준의 단위를 동화하여 내재화된 행동(interiorized actions)²을 보일 때 ‘n단계에서 조작한다’고 하였다. 이때 학생이 ‘n수준 단위를 주어진 자원으로 사용하여 동화할 수 있다’는 것은 문제 상황에서 실제 어떤 활동을 수행하지 않고도 n개의 단위 수준을 한 번에 설명하고 구별할 수 있음을 의미한다. 반면 ‘활동을 통하여 n수준을 생성한다’는 것은 학생이 정신적 또는 물리적으로 어떤 활동을 수행하여야 비로소 n개의 수준을 구성할 수 있으며, 활동 중에 n수준의 구조를 유지하지 못할 수도 있다(Norton et al., 2015). 이에 본 연구는 면담 과정에서 학생이 문제 상황을 해석하는 방식에 따라 나타나는 단위와 수준을 식별하고, ‘활동을 통해’ 3수준 단위를 생성하는지 또는 3수준 단위를 ‘주어진 자원으로’ 동화하여 내재화할 수 있는지를 판단하기 위한 척도로 단위 조정 단계에 대한 선행 연구를 살펴보고자 한다.

단위 수준과 단위 조정 단계에 대한 이해

Steffe (2010)은 오랜 교수실험을 통하여 학생들의 수세기 활동으로부터 관찰되어지는 행동과 표현을 통해 자연수 지식에 대한 모델로서 수세기 스킴을 제시하였는데, 네 가지 스킴인 Initial number sequence (INS), Tacitly nested number sequence (TNS), Explicitly nested number sequence (ENS), Generalized number sequence (GNS)로 구분하였다. Steffe의 단위 조정 수준에 대한 이전 연구들을 바탕으로 Hackenberg와 Tillema (2009)에서는 정수의 곱셈적 개념(Multiplicative Concept, [MC])에 대한 이해를 세 가지 MC1, MC2, MC3로 제시하였다. Ulrich (2015, 2016)에 의하면 Steffe의 네 가지 스킴 중에서 TNS, ENS, GNS는 곱셈적 개념(MC1, MC2, MC3)에 대한 단위 구조와 일대일 대응 관계가 있으며, 이를 ‘산술적 단위(arithmetical units), 합성 단위, 1의 반복 가능한 단위(iterable units of 1), 반복 가능한 합성 단위’라는 단위의 유형을 통해 설명하였다. 한편, Steffe의 단위 조정을 바탕으로 Norton 외 (2015)는 학생들이 동화시킬 수 있는 단위의 수에 따라 단계적으로 결정되는 학생들의 단위 조정의 능력을 특징지어 세 단계로 나누어 제시하였다. 짧은 막대, 중간 막대 및 긴 막대가 주어지고 짧은 막대가 중간 막대에 3번, 중간 막대가 긴 막대에 4번 맞는다고 할 때, 짧은 막대가 긴 막대에 몇 번 들어가는지 결정해야 하는 과제를 통하여 학생들의 단위 조정에 대한 조작 방식의 설명은 Table 1과 같다.

Table 1에서 단위 조정 단계에서의 학생의 단위 구조를 비교해서 살펴보면 단위 조정 1단계 학생은 1-막대가 가장 긴 막대에 12번 반복되어 셀 수 있는 것으로 1과 1의 반복인 12 전체를 생성할 수 있다. 반면 단위 조정 2단계 학생은 활동을 통하지 않고도 긴 막대 12가 1의 12번의 반복으로 전체를 이룬다는 것은 이미 알고 있는 상태에서 중간 막대 3을 4번 반복하는 활동을 통해 1-3-12의 3수준을 생각할 수 있다. 그러나 이 과정이 즉각적으로 이루어지는 것은 아니며, 중간 막대 3이 짧은 막대 3개의 1로 된 단위라는 사실로부터 이 합성 단위 3을 4번 실제로 반복하는 활동으로 가능한 것이다. 한편, 단위 조정 3단계로 3수준 단위를 주어진 자원으로 사용하여 동화할 수 있는 학생은 ‘단위의 단위의 단위(a unit of units of units)’인 3수준 단위 구조 안에서 구체적인 활동을 하지 않고도 단위 조정이 가능하다(Norton et al., 2015). 따라서 긴 막대를 4개의 중간 막대로, 중간 막대를 3개의 짧은 막대로 하여 단위의 단위의 단위로 주어진 관계인 1-3-12를 동화시킬 수 있다. 이 과정에서 신체적 혹은 정신적으로 반복적인 행동을 할 필요 없이 주어진 두 관계의 곱셈적 조정으로서 미지의 관계를 즉각적으로 파악할 수 있다는 점이 단위 조정 2단계 학생과의 차이이다.

본 연구에서 주목한 3수준 단위 조정과 관련하여 Norton 외 (2015)의 단위 조정 3단계 학생의 단위 구조는 Steffe (2010)의 GNS 및 Hackenberg와 Tillema (2009)의 세 번째 곱셈적 개념(MC3)과의 관계가 있음을 알 수 있다. Steffe의 GNS 개념 구성이 3수준 단위를 조정하여 상황을 동화할 수 있다고 할 때, Hackenberg와 Lee (2015)는 세 번째 곱셈적 개념(MC3)의 구성을 “주어진 자원으로 3수준의 단위를 사용하고 3수준의 단위 구조 간에 유연하게 전환하는 능력”(p. 206)과 유사하다고 특성화하였다. 따라서 합성 단위의 합성 단위의 동화적 특성과 3수준 단위 구조 사이의 유연한 전환 능력에서 이를 주어진 자원으로 하여 3수준 단위를 취하는 것은 동화된 구조 안에서 재귀적인 조작 활동에 해당되며 따라서 MC3와 GNS의 구성이 동시에 발생되는 것으로 이해할 수 있다(Ulrich, 2016).

분수 맥락에서의 단위 조정

학생들은 주어진 대상을 동일하게 분할하는 정신적 활동을 수행하면서 단위를 생성하고 조작하는 방식으로 분수 개념을 발달시켜 나아간다(Steffe & Olive, 2010). 이 과정에서 단위 조정 활동은 측정 결과로서 분수 개념을 발달시키고, 가분수 개념을 포함하여 상위 분수 지식을 구성하는데 중요한 기반이 된다(Norton & Boyce, 2015). 예를 들면 $\frac{7}{5}$이라는 가분수는 $\frac{1}{5}$의 7-단위로 그중 5-단위가 전체를 구성하는 하나의 양이 되어 학생들은 단위분수($\frac{1}{5}$), 전체($\frac{5}{5}$) 및 여러 단위분수와 관련하여 그 자체로 단일한 양을 인식하게 되는데, 이때 학생들이 다양한 수준의 단위를 생성하고 조정하는 조작 방식으로부터 그들의 단위 조정 단계를 암시해 준다. 따라서 분수가 포함된 문제 상황에서의 단위 생성과 단위 조정 활동에서의 다양한 조작들에 대해 구체적으로 살펴보고자 한다.

분수가 포함된 문제 상황에서 강조하는 조작은 부분 또는 전체를 몇 개의 동일한 조각으로 분할(partitioning)하고, 부분과 전체를 동일한 조각으로 나타내어 전체를 잃지 않은 상태에서 전체로부터 부분을 분리(disembedding)하여 반복(iterating)하고 더 큰 양을 구성하는 활동을 포함한다(Hackenberg & Lee, 2015; Steffe & Olive, 2010). 이 과정에서 분할은 그 자체가 분수 지식의 구성 과정에 중요한 역할을 하며, 분할한 부분에 대한 분리 조작과 분리한 부분의 반복을 통해 다시 전체를 구성하는 반복 조작은 분수 지식의 기본 조작이 된다. 분할, 분리, 반복이라는 기본 조작은 이들의 결합을 통해 순차적으로 수행할 수 있는 등분할 조작과 이를 동시에 수행할 수 있는 좀 더 발전된 스플리팅 조작(splitting operations)으로 구분되는데(Steffe, 2001), 스플리팅 조작은 가분수를 구성하는데 핵심 조작이며, 곱셈적 관계를 가역적으로 추론하기 위해서도 필요하다. 한편, 등분할 조작은 부분 분수 스킴의 활동을 수행하는 조작을 통해, 그리고 스플리팅 조작은 반복 분수 스킴의 활동을 수행하는 조작을 통해 각각 식별되고, 등분할 조작과 스플리팅 조작은 분수에서의 두 스킴인 부분 분수 스킴과 반복 분수 스킴 간의 차이로부터 기인한다고 본다(Shin & Lee, 2019). ⁵

이때 Steffe (2003)은 부분 분수 스킴 이상의 분수 스킴의 구성으로부터 재귀 분할(recursive partitioning)이 나타난다고 보고, 전체를 부분으로 분할하는 활동에서 부분의 부분과 전체 사이의 관련성으로부터 재귀 분할에 대한 조작의 구성을 설명하였다. 재귀 분할은 두 분할의 합성을 통하여 합성 단위를 생성하고 여러 개의 단위 조정으로 전체를 새로운 3수준 단위의 양적 구조로 바라볼 수 있는 정신적 활동이다. 따라서 재귀 분할은 동치 분수를 구하거나 분모가 다른 분수의 크기를 비교하기 위해 공통인 측정 단위를 구성하여 전체와의 관계를 형성할 수 있도록 하며(Shin & Lee, 2019), Lee와 Pang (2016)에서는 재귀 분할을 분모가 다른 분수의 덧셈과 뺄셈의 중요한 조작으로 강조하였다.

또한 Steffe (2003)은 자연수와 관련된 곱셈 스킴이 재귀 분할을 통해 분수의 곱셈 맥락에서 작동하게 되는데, 부분의 부분과 전체 사이에서 나타내는 곱셈적 관계로부터 분수 개념의 구성을 설명하였다. 그리고 이 과정에서 부분의 부분이 전체의 양으로 돌아가기 위해서는 가역성이 수반된다고 보았다. 결과적으로 Steffe에 의하면 2수준 단위 구조의 내재화(즉, 활동을 통해 3수준 단위 구성)가 재귀 분할에서 필수적인 요소라는 것이다. 그리고 Yoo와 Shin (2021)은 더 나아가 가역성에 대한 구성이 문제 상황에서 재귀 분할을 수행 가능하게 한다고 하였다. 따라서 자연수 지식이 분수 지식에 가용되기 위해서는 가역성이 수반되어야 하며, ‘활동을 통해’ 3수준 단위를 생성하는 단위 조정 2단계 학생의 능력과 관련됨을 시사하고 있다. Steffe의 연구로부터 Yoo와 Shin (2021)은 자연수에서 단위분수 조정으로의 연결은 스플리팅 조작으로 가능하며, 이는 재귀 분할의 수행이 내재화되기 위한 과도기적 변화의 중요한 요인으로 보았다. 그리고 스플리팅 조작을 동반한 가역성은 분수 맥락의 문제 상황에서 재귀 분할의 내재화와 관련됨을 통해 Steffe (2003)의 연구 결과를 확증하였다. 한편, Kim 외(2018)에서는 자연수 지식과 분수 지식의 연결 과제로써 균등 분배 문제 상황에서 합성 단위에 대한 스플리팅 조작과 분배 분할 조작을 통해 학생들의 문제 해결 과정에서 보여지는 다양한 전략들을 분석함으로써 단위 조정의 역할을 강조하였다.

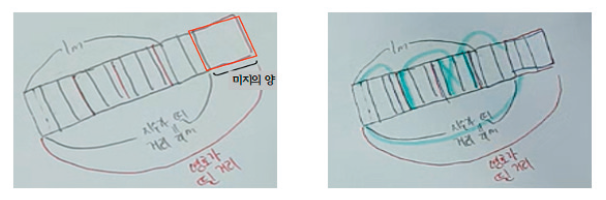
앞서 선행 연구들 정리해보면 자연수의 곱셈 맥락에서 보여준 재귀적 조작 활동이 분수의 곱셈 맥락에서 작동하는 재귀 분할의 수행에 영향을 미치며, 단위 조정 수준과 단계에 따라 스플리팅 조작, 합성 단위에 대한 스플리팅 조작, 분배 분할 조작이 각기 다른 방식으로 학생의 문제 해결 과정에 관련될 수 있음을 보여주었다. 따라서 본 연구에서는 같은 단위 조정 3단계인 두 학생의 분수 의 곱셈 맥락에서 나타나는 문제 해결 과정에 대한 분석을 설명해줄 수 있는 단서로써 합성 단위에 대한 등분할 조작, 합성 단위에 대한 스플리팅 조작과 분배 분할 조작에 주목하고자 한다. 합성 단위에 대한 스플리팅 조작은 Hackenberg (2010)에서 가역적 곱셈 관계 문제를 해결하기 위한 핵심 조작으로 설명하였으며, 등분할 조작과 스플리팅 조작이 ‘단일 단위에 대한 분할’에 기인한다면 합성 단위에 대한 등분할 조작이나 합성 단위에 대한 스플리팅 조작은 ‘합성 단위에 대한 분할 조작’에서 정의할 수 있다. 예를 들면 높이가 65 cm인 탑처럼 쌓은 CD 더미가 있다. 이는 구하고자 하는 CD 더미 높이의 5배라고 할 때, 합성 단위에 대한 등분할 조작을 구성한 학생은 전체 양을 동일한 미지의 양의 5개로 구성된 3수준 단위 구조로 65를 상상할 수 있다. 이를 바탕으로 주어진 CD 더미를 다섯 부분으로 분할하는 조작을 수행하게 되는데, 그 결과로 얻은 다섯 부분 중의 한 부분에 들어갈 CD 더미의 높이는 13 cm를 5번 반복하여 원래 CD 더미인 65 cm를 구성함으로써 13이 65의 $\frac{1}{5}$임을 확인할 수 있다. 한편 합성 단위에 대한 스플리팅 조작은 한 수준 높은 단계의 분할 조작으로 65의 $\frac{1}{5}$을 바로 해결할 수 있을 뿐만 아니라 3의 $\frac{1}{5}$의 문제 상황도 분할하여 더 작은 부분으로 만들 필요성을 느낄 수 있다.⁶

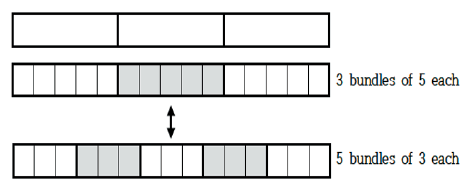
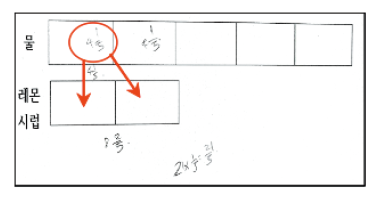
Figure 1에서와 같이 3-막대에 각각 5를 합성하여 5개씩 세 부분인 15개로 변환할 수 있고, 동시에 15개 중 3개의 5번 반복으로 전체를 인식할 수 있다. 이 과정이 순차적이 아니라 동시에 수행되며 실제 분할 활동 없이 정신적 수행이 가능하다는 점이 합성 단위에 대한 등분할 조작을 구성한 학생과 합성 단위에 대한 스플리팅 조작을 구성한 학생 간의 차이점이라고 볼 수 있다. 3의 $\frac{1}{5}$에 대한 문제 상황은 또 다른 조작인 분배 분할 조작(distributive partitioning operations)으로도 가능하다.

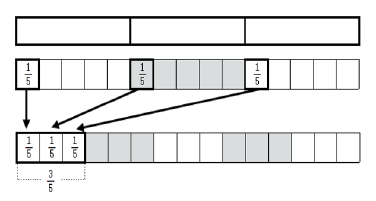
분배 분할 조작에서는 3-막대에 각각 5를 합성하여 Figure 2에서와 같이 전체 3의 각 부분에서 단위분수 $\frac{1}{5}$만큼의 양을 부분의 수만큼 모아 $\frac{3}{5}$이 된다고 생각할 수 있다. 따라서 문제 상황에 대한 이해 측면에서 합성 단위에 대한 스플리팅 조작과 같이 주어진 전체 양에 새로운 단위를 합성 단위로 분할한다는 공통점이 있다. 그러나 분배 분할 조작은 세 부분인 1 각각에 대하여 $\frac{1}{5}$씩 분배하는 것으로 이해한다면 부분의 양을 단순히 분할하기만 하는 것이 아니라 부분의 양에 대한 단위분수만큼을 택한다는 인식이 분할 조작 과정에 수반되어야 하며(Hackenberg & Tillema, 2009; Kim et al., 2018), 각 부분에서 단위분수를 택하여 그 양을 반복하는 것을 포함한다. 따라서 Hackenberg와 Tillema (2009)는 분배 분할 조작이 일반화된 분수 합성 스킴(generalized fraction composition scheme)을 구축하는데 필요한 조작임을 강조하였다.

초등 수학에서 분수는 수 세기를 통해 도입된 자연수 개념을 분수로 확장하여 사칙연산을 정의하는데 그 과정적 목표를 두고 있다. 이후 중등 수학에서는 분수를 포함하여 수 개념을 대수적 측면에서 해의 존재를 보장하기 위한 확장된 개념으로 즉, 대수로의 이행을 위한 수학 학습을 위한 기초적 개념으로 접근하고 있다(Ministry of Education, 2015; Suh, 2020). 따라서 분수에서의 단위 조정 조작 방식과 대수 추론의 전제 조건인 비례 추론 사이의 관계를 이해하는 것은 이후 초등 산술로부터 대수적 사고로의 전환 시기에서 학생들이 무엇을 이해하고 있는지에 대한 분석의 도구가 될 것이다.

비례 개념과 관련한 선행 연구

비례 추론은 고등 수학의 초석이자 초등 수학의 반석이라고 여겨질 만큼 학생의 수학적 발달에 중요한 역할을 감당하고 있다(Lesh et al., 1988). 학생들의 비, 비율과 비례 관계에 대한 이해를 바탕으로 관련된 문제를 해결하는 능력을 비례 추론이라 할 때, 학생이 ‘비, 비율과 비례 개념을 이해한다’는 것은 문제 상황에서 단순히 두 대상의 곱셈적 관계를 ‘a : b’로 표현하거나 비를 $\frac{a}{b}$와 같은 비의 몫으로써 이해하는 것뿐만 아니라, 두 비의 몫 $\frac{a}{b}$와 $\frac{c}{d}$를 비교하고 두 비가 같음을 ‘a : b = c : d’로 표현하는 것 그 이상의 의미를 가진다(Chong, 2015).

Thompson (1994)에 의하면 비는 두 양의 곱셈적 비교에 대한 결과로, 비율은 두 양의 곱셈적 비교 결과로부터 반영적 추상화한 ‘내재화된 비’로 보았다. 그리고 Thompson의 내재화된 비 개념에서 Johnson (2015)는 이를 구체화하여 ‘하나당으로의 비’와 ‘측정으로의 비’로 식별하였다. 한편, 비를 두 대상의 곱셈적 관계에 대한 의미로 보았을 때, 비례는 두 비가 같음을 의미하는 것으로 비와 구분하여 사용하지만, 공변하는 두 양 사이의 변하지 않는 곱셈적 관계인 양의 공변과 비의 불변이라는 네 양 사이의 구조적 관계로서도 그 의미를 가진다(Lamon, 2007). 따라서 비례 개념에 대한 양 사이의 구조적 관계를 이해하는 것은 중등 수학 과정에서 도형의 닮음과 삼각비, 함수의 기울기와 같은 보다 높은 수준으로의 수학적 지식을 형성하는데 중요한 기반이 된다(Lamon, 2007; Lobato et al., 2010).

비례 개념과 관련하여 국내외 선행 연구들을 살펴보면 크게 두 가지 방향성을 가진다. 우선 첫 번째 비, 비례 개념 및 정의를 수학적으로 분석한 연구이다. 비, 비율에 대한 용어의 정의(예, Hong, 2013; Jeong, 2003a; Park, 2010), 비, 비례 추론의 의미와 요소의 분석(예, Chong, 2015; Jeong, 2003b, 2013), 비례 추론의 핵심적 요소를 바탕으로 교과서 분석을 통한 비례 추론 지도에 대한 논의(예, Chong, 2015; Jeong, 2013; Kim & Na, 2008; Kim & Paik, 2010; Kwon et al., 2007), 비례 추론의 핵심적 요소에 대한 인식을 강조한 연구(예, Lobato et al., 2010; Shin & Lee 2019; Thompson &Salbanha, 2003) 등이 있다. 이러한 관점에서의 연구는 비례 개념을 수학의 다른 영역으로 확장·적용되기 위한 발판이 되며, 초등 수학에서 수와 연산 특히, 분수의 곱셈에 대한 의미로부터 중학교에서 비, 비례 추론의 이해에 중요한 토대가 될 수 있다.

그러나 학생들의 수학은 완성된 형식적 체계를 갖춘 학문적 수학과는 차이가 있기 때문에(Steffe, 2001), 비례 문제 해결 과정에서 학생들의 전략과 비례 추론 능력의 발달을 위해서는 그 과정에 대한 실증적인 질문과 면담을 통해 질적 자료에 근거한 연구가 뒷받침될 필요성이 요구된다(Behr et al., 2013; Kaput & West, 1994; Thompson, 1994).

학교 수학에서 비, 비례 개념을 지도할 때 학생들에게 형식적 절차를 강조하는 경우가 많고(Jeong, 2013; Lesh et al., 1988), 실제로 학생들의 비, 비례 개념과 관련한 문제 해결 과정을 살펴보면 형식적인 알고리즘 계산에 치중하여 자신이 구한 답의 양적 의미에 대한 이해가 뒷받침되지 못하는 경우들도 있다(Eom & Kwean, 2011; Ko & Lee, 2007; Lobato et al., 2010). 이는 비례 관계에 대한 학생들의 적절한 이해를 보장할 수 없다. 따라서 비례 개념에 선행 지식인 자연수나 분수 지식 등을 활용한 비형식적 해결 과정에 초점을 두어 학생들의 비례 문제에 대한 이해와 문제 해결 과정에서의 비례 추론 방식에 대한 연구가 강조되고 있다.

이에 두 번째는 보다 실증적인 분석을 바탕으로 인지 주체인 학생의 추론 방식을 이해하려는 연구이다. 주로 초등학생을 대상으로 다양한 문제 상황에서 비례적 사고에 영향을 미치는 요소(예, Ko &Lee, 2007), 비례 문제 해결 과정에서 나타나는 전략에 따라 학생들의 비례 추론 능력에 미치는 영향(예, Carney et al., 2016; Park, 2008), 비구조화된 비례 문제 해결 과정에서의 경험에 따른 학생들의 비례 추론 수준 분석(예, Hong & Kim, 2013), 그리고 학생들의 학업 수준에 따른 비례 추론의 세부 능력 분석(예, Eom & Kwean, 2011) 등의 연구들이 있다. 또 연구 대상을 초등학생에서 중학교 1학년 학생까지 비례 문제 관련 검사지를 이용해 문제 유형별, 학년별 학생들의 반응과 오류를 분석한 연구(예, Ahn & Pang, 2008)도 있다. 그러나 이들 대부분은 비구조화된 문제를 포함하여 다양한 비례 문제 상황에서 학생들의 문제 해결 과정에 나타나는 전략이나 오류 분석에만 초점을 두고, 어떠한 정신적 활동이 실행되었는지 구체적으로 언급한 연구는 드물다. 그리고 수준(혹은 단계) 안에서 나타나는 다양한 전략들 사이에 어떤 관계가 있는지도 불분명하다는 한계를 가진다. 이러한 방향적 접근이 학생의 비례 개념에 대한 구성 및 문제 해결 과정에 대한 구체적인 도움을 주기 위해서는 학생의 입장에서 정신적인 조작을 통해 양을 구성해 나아가는 과정적 측면으로의 연구가 더해질 필요가 있다.

이에 본 연구는 두 번째 방향에 초점을 두고 학생들이 다루는 양들 사이 관계에 주목하여 비례 문제 해결 과정에서 학생들이 어떠한 방식으로 접근하는지 구체적으로 연구하고자 한다. 학생 자신이 구성하고 있는 경험 세계와 상호작용하는 과정에서 나타나는 스킴과 조작으로 비례 추론을 본다면, 결국 비례 추론은 두 양 사이의 곱셈적 비교를 통해 관계를 설정하고 이를 다른 두 양의 관계로 확장하여 필요한 스킴과 조작들을 문제 상황에서 원활하게 작동시킬 수 있는 능력으로 정의된다(Lamon, 2007; Shin & Lee, 2019).

최근 들어 비, 비례 문제에 대하여 자연수, 분수의 연산과 같은 초등 산술에 대한 지식의 구성이 학생들의 문제 해결 과정에서 어떻게 관련되는지 주목하고 있다(예, Lee & Shin, 2020; Liss II, 2019; Nabors, 2003; Shin et al., 2020). 비, 비례 문제와 분수 지식의 연관성을 살펴본 연구로 Nabors (2003)는 분수 지식과 관련된 과제를 해결할 때 학생들이 사용할 수 있는 조작 방식이 비례 문제가 포함된 과제 해결에 사용되는 전략과 조작의 기초를 형성한다고 보았다. 한편, Liss II (2019)는 학생들의 분수 지식과 관련된 문제 해결 과정에서 여러 수준의 단위 구조로 추론하는 능력을 ‘분배 공유 스킴, 분배 분할 스킴, 가역적 분배 분할 스킴’이라는 세 가지 스킴으로 그 차이를 설명하였는데, a : b의 비에서 기준량에 대한 비교하는 양으로의 단위 비(unit ratio)와 같은 내포량에 대한 양적 조작은 가역적 분배 분할 스킴에 의해 가능함을 제안하였다. 그러나 두 선행 연구는 비, 비례 개념과 관련된 문제를 해결하는데 분수 스킴이 중요한 역할을 하지만 구체적으로 무슨 조작이 어떻게 문제 해결을 구성하게 되는지에 대한 분석이 부족하였다.

구체적인 ‘조작’에 초점을 두며 학생들의 문제 해결 과정에 주목한 또 다른 연구로는 Lee와 Shin (2020)과 Shin 외 (2020)가 있다. Lee와 Shin (2020)은 비에 대한 양적 구조가 단위 조정 단계에 따라 어떠한 차이가 나타나는지를 단위 조정 2, 3단계 학생들을 대상으로 단위 조정 2단계 학생은 같은 비라 하더라도 맥락에 따라 다른 단위 구조를 표상하여 사용할 수 있고, 단위 조정 3단계 학생은 ‘비율이 같은 비의 집합’으로서 동치 비 개념을 구성하는 것과 관련이 있음을 확인하였다. 한편 Shin 외 (2020)는 ‘활동 이전’과 ‘활동을 통해서’ 두 개의 3수준 단위 구조를 조정하는 학생을 대상으로 비례 문제 해결 과정에서 단위 조정의 결과적 차이를 확인하였고, 이러한 차이로부터 비례 추론을 구성하기 위해서는 두 개의 3수준 단위 구조를 조정하여 합성 단위에 대한 스플리팅 조작이 필수적임을 나타내며, 두 개의 3수준 단위의 동화된 구조에서 합성 단위에 대한 스플리팅 조작을 수반할 때 Liss II의 연구 결과도 가능함을 시사하였다.

본 연구는 이와 같은 맥락에서 학생들이 다루는 양들 사이 관계에 초점을 두고자 한다. 그러나 앞선 연구들이 단위 조정 단계가 다른 학생들의 문제 해결 과정에서의 차이에 따라 비례 문제 해결 과정에서의 그 결과적 차이에 초점을 두고 있다면, 학생들이 문제 해결 과정에서 같은 전략을 사용하여 같은 결과가 나왔다 하더라도 조작적 관점에서 학생들의 사고 과정은 다를 수 있다고 본다. 따라서 3수준 단위 조정이 가능한 학생들을 대상으로 어떠한 조작 활동이 비례 문제 해결 과정에 어떠한 역할에 기여하는지 비례 문제 상황에 대한 양적 조작 방식을 분석하여 보고자 한다.

연구 방법

연구 방법 개관

본 연구에서 수집된 자료는 중학교 1학년 4명을 대상으로 2021년 5월부터 2021년 8월까지 30∼50분씩 학생당 7차시(총 28차시)에 걸쳐 진행된 임상 면담(Clement, 2000)에 대한 자료 일부이다. 임상 면담의 목적은 자연수, 분수 지식과 비례 관련 문제 상황으로부터 대수식 표현에 대한 관계를 이해하는 것이었고, 일부의 면담 자료인 분수 지식과 비, 비례 관련 문제 상황에서 학생의 추론 과정에 대한 이해를 본 연구의 초점으로 두었다. 모든 면담은 학교 도서관에서 방과 후에 본 고의 저자 중 한 명인 교사(면담자)와 학생이 일대일로 면담을 진행하였다. 면담자는 미리 계획된 과제와 준비된 질문들로 면담을 진행하되 학생의 답변이 모호할 경우 학생의 생각을 세밀히 관찰하기 위해 질문지에 없는 질문을 하기도 하였다. 그리고 과제 해결에 직접적인 도움은 주지 않는 범위 안에서 추가 질문 등을 통해 상호 작용하였으며, 질문에 대한 풀이 시간은 학생들의 차이를 고려하여 충분히 부여하였다.

연구 대상 및 과제 소개

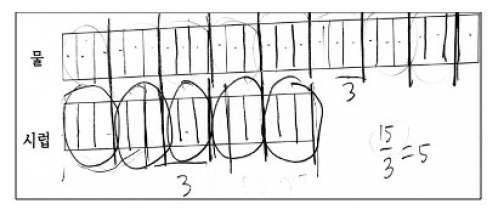
다양한 수학적 수준의 학생들을 선정하기 위해 경기도에 소재한 한 중학교 1학년 수학 담당 교사의 도움으로 수업 중 이루어진 단원별 형성평가 점수와 자발적 참여 의사를 고려하여 현재 사교육을 받고 있지 않은 학생을 대상으로 학부모 동의를 거쳐 4명을 면담 참여자로 선정하였다. 이는 COVID-19의 단계별 학생 등교 상황에 따라 원격수업 기간에도 수업 후에 학교로 등교하여 면담이 진행된다는 점을 고려할 때 성실히 참여할 수 있는 연구 대상자를 선정하는 것이 중요하다고 판단했기 때문이다. 4명의 학생은 1차 사전면담을 통하여 단위 조정 단계의 관점에서 2수준 단위를 주어진 자원으로 사용할 수 있는 2단계 학생 1명과 3수준 단위를 주어진 자원으로 사용할 수 있는 3단계 학생 3명으로 판단되었다. 특히 본 연구는 단위 조정 3단계 학생 3명 중 문제 해결 과정에서 설명과 그린 그림이 유사했던 두 명의 학생인 상연과 혜지에 주목하였다. 1차 사전면담 과정에서는 6개씩 4줄과 6개씩 8줄로 된 쿠키가 들어있는 상자가 있을 때 두 상자를 합하면 쿠키가 총 몇 개가 있는지 물어보았다.

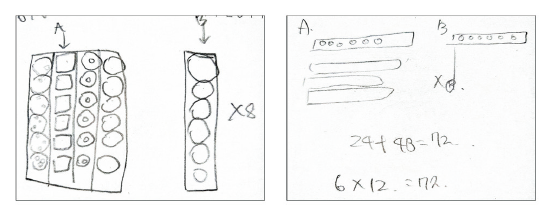
이때 상연과 혜지는 Figure 3과 같이 유사한 그림을 그리며 “6×4+6×8”과 “24+48”이라는 식을 통해 “72”라고 답하였다. 그리고 다른 풀이가 있는지에 대한 면담자의 질문에서도 두 학생 모두 4줄과 8줄이면 12줄이므로 “6개씩 12줄”이라고 표현하였다. 또한 한 줄에 4개씩 6줄로 된 의자에 추가로 12개의 의자를 늘렸다면 의자가 모두 몇 개인지 물어보는 문제에서 상연은 “12는 4개씩 3줄이므로 총 9줄이라서 4개씩 9줄이면 36개”라고 답하였다. 한편 혜지는 쿠키 문제와 같이 4개의 의자를 가로에 그리고 “×6”이라고 활동지에 적으며 24개에 12개를 더하면 36개라고 하였다. 면담자가 또 다른 풀이가 있는지 물어보자 혜지는 12개의 의자를 4개씩 3줄로 하여 9줄에 4를 곱해 총 의자 수를 답하였다. 두 학생 모두 문제 상황에서 ‘6개씩’과 ‘4개씩’을 각각 한 단위로 하여 ‘6개씩 총 12줄’과 ‘4개씩 총 9줄’인 문제 상황으로 보고, 전체 72개의 쿠키와 36개의 의자 수를 즉각적으로 답할 수 있었으며 두 문제를 모두 곱셈적 관계가 포함된 상황으로 이해하였다. 두 과제로부터 구성한 단위와 단위 조작 방식을 정리해보면 활동 이전에 n-단위 m묶음(단위의 단위)과 n-단위 k묶음을 더하여 전체 (nm+nk)개라고 생각할 수 있고, 1-n-nm, 1-n-nk라는 3수준 단위 구조를 유지하면서 동시에 전체 (nm+nk)개로부터 이전의 단위인 n-단위를 취하여 n-단위 (m+k)묶음으로 1-n-n(m+k)라는 새로운 3수준 단위 구조를 재구성할 수 있었다. 그리고 이러한 단위 조작이 모두 활동을 통해서 보여진 것이 아니라 이전에 가능했던 것으로 보인다. 따라서 두 학생 모두 자연수 맥락에서 단위 조정 3단계 학생으로 판단되었다. 본 연구는 같은 단위 조정 수준에 있는 두 학생이 가분수가 포함된 분수 맥락에서 나타내는 단위 조정 활동과 조작 방식에는 어떠한 공통점과 차이점이 있는지를 통해 비례 문제 해결 과정에서 어떠한 관련성을 보여주는지 자세히 분석해보고자 한다.

면담에 대한 과제의 전체 구성 방향은 대상 학생들이 가지고 있는 자연수와 분수 지식, 비례 지식과 비례 개념이 포함된 대수적 지식이 잘 나타나도록 과제를 선정하는 것이었다. 학생들의 자연수 지식과 분수 지식과 관련한 연구(Hackenberg & Tillema, 2009; Hackenberg, 2010; Kim et al., 2018; Shin et al., 2020; Yoo & Shin, 2020, 2021), 비례 관련한 연구(Lamon, 1993; Lee & Shin, 2020; Shin & Lee, 2019; Shin et al., 2020), 식의 표현과 관련한 연구(Hackenberg & Lee, 2015; Lee & Lee, 2020) 등을 참고하여 총 30개 이상의 과제를 재구성하여 학생의 반응에 따라 한 차시에 4~5개의 과제를 다루었다. 또한 학생들이 다루게 될 과제는 사전에 선정하여 면담 계획에 따라 제시하였다. 본 연구에서는 학생들의 분수 지식과 비례 개념에 대한 이해에서 보여준 단위 조정과 관련한 조작 활동을 분석하고자 하였으므로 총 7차시 30개 이상의 면담 과제 중 두 차시 총 8문제에 대한 학생들의 문제 해결 과정을 분석하였다.

Table 2의 분수 지식과 관련된 연구는 Hackenberg와 Tillema (2009)에서 5가지의 유형으로 제시된 분수 곱셈 연산에 대한 과제이다. ‘단위분수의 단위분수(a unit fraction of a unit fraction), 단위분수의 진분수(a non-unit fraction of a unit fraction), 진분수의 단위분수 (a unit fraction of a non-unit fraction), 진분수의 진분수(a non-unit fraction of a non-unit fraction), 가분수의 가분수(complex fraction composition)’와 관련한 분수 곱셈의 5가지 유형으로 양적 구조는 유지하되 우리나라 상황에 맞추어 재구성하였다. 분수 곱셈의 형태로 분수 구성 문제에 주목하여 합성 단위에 대한 스플리팅 조작 및 분배 분할 조작과 같은 보다 정교한 분할 조작을 유발할 것으로 예상하였으며, 특히 Hackenberg와 Tillema에 의하면 ‘비 단위분수의 비 단위분수’는 최소한 3수준 단위를 활동을 통해 구성해야 문제 해결이 가능하다고 하였다. 또한 3수준 단위를 내면화한 단위 조정 3단계 학생이라면 분수 맥락 안에서 분배 분할 조작을 통하여 가분수를 포함한 비 단위분수의 비 단위분수의 양을 추론할 수 있다고 보았다.

다음은 Table 3에서와 같이 비례 관계와 관련된 과제이다. Lamon (1993)은 비례 개념을 포함 문제 상황들을 분석하여 의미적 유형을 4가지로 구분하였다. 첫 번째 유형인 양의 측정(well-chunked measures)은 두 개의 외연량을 비교해 내포량을 얻는 것을 말한다. 두 번째 유형은 부분-부분-전체(part-part-whole)로 전체 안에 포함되어 있는 두 부분집합의 외연량을 비교하는 것이다. 세 번째 유형인 관련된 집합(associated sets)은 문제 상황에서 정의되기 전에는 관련이 없던 두 요소 사이의 관계를 비교하는 것으로 예를 들면 사람 수와 피자 조각의 수와 같은 것을 말한다. 네 번째 유형인 확대와 축소(stretchers and shrinkers)는 두 특성을 나타내는 두 양의 확대, 축소 상황으로 닮음이 여기에 해당된다. 본 연구에서는 첫 번째와 네 번째 유형으로 비례 관계에 있는 문제 상황을 제시하였다. 총 5개 과제 중 자연수 배수 관계 여부와 막대 그림의 제시 여부를 통해서 본 연구에서 분석한 과제는 3개 과제이며, 그중 마지막 과제는 닮은 도형과 관련된다. ‘도형의 닮음’은 중학교 2학년에서 배우는 개념이기 때문에 면담자는 ‘닮은 도형’이라는 표현을 면담 중에 사용하지 않았고, 학생들에게 익숙한 휴대폰의 이미지 확대-축소 기능에 대한 설명을 통해 학생들이 문제 상황을 이해할 수 있도록 하였다.

자료 수집 및 분석 방법

각 면담은 학생과 면담자가 같은 방향으로 나란히 앉아 진행되었으며, 면담의 모든 과정은 카메라로 녹화되었다. 차시별로 촬영된 영상, 면담 내용에 대한 전사 자료, 학생 활동지, 그리고 촬영된 영상 안에서 관찰된 학생의 특징을 기록한 일지 등 포함하여 분석에 종합적으로 활용하였다. 분석은 두 단계로 진행되었는데, 1차 분석은 면담이 진행되는 과정 중의 자료 수집과 분석이 동시에 이루어졌으며, 2차 분석은 모든 자료 수집이 완료된 이후에 회고 분석을 실시하였다. 1, 2차 분석으로부터 연구 문제에 부합하는 결과를 도출하고자 하였다. 1차 분석의 목적은 분수 관련 문제와 비례 문제 해결 과정에 대한 개별 분석을 위해 학생과 면담자와의 대화 중에 관찰되는 언어적 표현과 비언어적 표현(손동작, 표정, 기타 행동 등)이 학생들의 문제 해결 과정에서 어떤 수학적 구조와 조작들을 기반으로 사고하여 행동하는지를 추론하고 기술하는 것이었다(Yoo et al., 2018). 이 단계는 학생 면담 과정에 대한 발췌문을 포함하여 문제 해결 과정에 대한 해석과 추측, 선행 연구로부터의 이론적 틀을 바탕으로 기술된 연구자의 분석으로 구성되었다(Corbin & Strauss, 2015). 2차 분석은 1차 분석의 결과를 바탕으로 두 저자가 논의를 통해 두 학생의 분수 지식과 비례 지식 사이에서 보여진 조작 방식을 일관성 있게 설명할 수 있는 요소를 찾아 학생들의 단위 조정 활동과 추론 과정에 대해 설명할 수 있는 가설을 세우고, 연구 문제를 확인하는 데 목적을 두었다(Ezzy, 2002).

결과 분석

두 학생의 분수 맥락에서의 단위 조정

과제 [F1], [F2], [F3]에 대한 분수 문제 상황에서는 두 학생 모두 결과적으로 면담자의 개입 없이 스스로 그림을 그려가며 문제를 해결해 나갔다. 이 과정에서 상연에게 나타난 일관된 모습은 수치적 계산을 먼저 한 뒤에야 그림을 그려서 자신의 답을 확인하는 모습이었다.

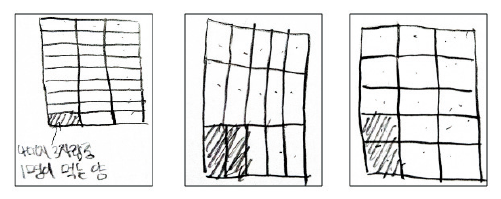
상연이 설명을 위해 그린 그림은 Figure 4와 같이 모두 m × n직사각형 형태(예, 3×9, 5×3, 3×5의 직사각형)로 구하고자 하는 부분을 색칠하며 수치적 계산으로 나온 값을 확인하였다.

반면 혜지가 그린 그림은 Figure 5와 같이 문제의 유형에 따라 조금씩 달랐다. 혜지는 ‘$\frac{1}{9}$의 $\frac{1}{3}$’과제에서 상연과 같이 m × n직사각형 형태(9×3 직사각형)로 한 칸을 색칠하며 $\frac{1}{27}$을 나타내었지만, ‘$\frac{1}{3}$의 $\frac{2}{5}$’과제에서는 1-막대를 3등분하고, 3부분 중 1부분만 (동일한 크기로의 분할이 아닌) 5등분하여 그중 두 칸을 색칠하며 $\frac{2}{15}$임을 설명하였다. 그리고 ‘$\frac{1}{3}$의 $\frac{2}{5}$’에서 1-막대를 3등분한 1부분($\frac{1}{3}$)을 1-단위로 하여 $\frac{2}{5}$를 택했던 것과 같이 ‘$\frac{2}{5}$의 $\frac{1}{3}$’과제에서도 1-막대를 5등분하여 5부분 중 2부분을 하나의 1-단위로 보고 $\frac{1}{3}$을 택하기 위해 다시 $\frac{2}{5}$(혜지에게는 1-단위)를 Figure 5의 세 번째와 같이 점선으로 3등분하여 한 칸을 색칠했다. 이후로 ‘$\frac{2}{15}$’라는 답을 말하기까지 혜지는 ‘30초’라는 시간이 걸렸다. 이 시간 동안 혜지는 $\frac{2}{5}$를 3등분한 한 칸을 다시 절반으로 나누었으며, 결국 1-막대 전체를 15부분으로 만들었다. ‘$\frac{2}{5}$의 $\frac{1}{3}$’은 1-막대를 5등분한 (각 $\frac{1}{5}$이 두 개인) 2부분의 $\frac{1}{3}$이므로 ‘2의 $\frac{1}{3}$’에 대한 문제 상황으로 인식할 수 있다. 따라서 더 작은 부분으로의 분할에 대한 필요성이 요구되며, 각 $\frac{1}{5}$에 3을 합성하여 전체 1을 $\frac{15}{15}$로 변환할 수 있어야 한다. 상연에게는 세 가지 유형의 문제 모두 수치적 계산 후 m × n직사각형 형태로 설명이 가능하였기에 같은 문제 상황이었을지 모르지만, 혜지에게는 ‘진분수의 단위분수’ 유형은 ‘더 작은 부분’으로의 분할이 요구되는 문제 상황으로 ‘30초’라는 고민의 시간이 필요했던 만큼 도전적인 문제 상황이었다.

다음으로 두 학생에게 제시된 유형은 조금 더 복잡한 문제인 ‘진분수의 진분수’와 ‘가분수의 가분수’ 문제이다. 제시된 문제는 1 m를 기준으로 한 ‘제자리 멀리 뛰기’ 상황이므로 상연이 지금까지 나타냈던 m × n직사각형 형태로는 더 이상 해결하기 어려운 문제였다. 따라서 수치적 계산으로 답은 구할 수 있을지 몰라도 두 가지 유형은 두 학생 모두에게 도전적인 문제 상황으로 면담자의 추가 질문에 의한 ‘활동을 통해’ 단위를 조정하는 모습을 보였다. 다음은 두 학생이 활동을 통해 보여지는 분할의 결과와 가용 가능했던 조작들을 단위 조정 관점에서 살펴보고자 한다.

분수 맥락에서 혜지의 단위 조정

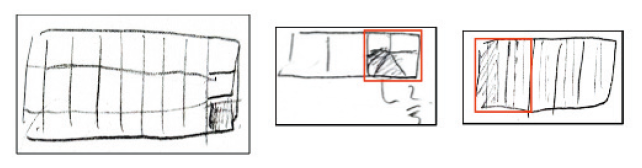
분수 맥락에서 혜지의 단위 조정 ‘진분수의 진분수’ 유형인 과제 [F4]에서 혜지는 1-막대(1 m)를 4부분으로 나누고, 4부분 중 3부분이 지수가 뛴 거리 $\frac{3}{4}$ m라는 것을 그림으로 나타내었다. 그리고 ‘지수가 뛴 거리로부터 영호가 뛴 거리’를 나타내기 위해 $\frac{3}{4}$ m인 3부분을 분할하기 시작하였다.

혜: (긴 직사각형을 그리고, 4등분한 것 중 3부분 빗금으로 색칠한 뒤 “지수”라고 적는다. 그리고 색칠한 3부분을 다시 절반씩 나눈다.) 어! (절반씩 나누었던 선을 지우고, 5초 뒤에 3개씩 나눈다. 3초 뒤 3개씩 나눈 것 중 두 번째와 세 번째 칸을 다시 절반씩 나눈다.)

혜지는 [F4]를 ‘3의 $\frac{2}{5}$’에 대한 문제로 인식한 것이다. 그러나 $\frac{1}{4}$부분을 5등분으로 바로 분할하지 못하고, Figure 6과 같이 분할 과정에서 여러 번의 시행착오를 보여주었다. 처음에는 지수가 뛴 거리 3부분을 모두 절반씩 나누더니 5초 뒤에 나눈 선을 지우고, 각각 3개씩 나눈 다음 3초 뒤에 3개로 나눈 것 중에 두 번째와 세 번째를 다시 절반씩 나누었다. 바로 5등분으로 분할하지 못하고, 5등분이 될 때까지 $\frac{1}{4}$-단위를 순차적으로 2개, 3개, 4개, 5개로 나누었다. 이후로 지수가 뛴 거리를 15부분으로 분할한 뒤 $\frac{2}{5}$를 나타내는 과정에서 혜지가 보여준 조작 활동에 주목해 볼 필요가 있다.

혜: (15부분에서 하나씩 손가락으로 집어가며 하나, 둘 세더니 잠깐 멈추고, 4번째 작은 칸의 선을 좀 더 진하게 긋더니, 15개의 칸 중 두 번째 칸까지 진하게 색칠하다가 2초가량 잠시 멈춘다. 그리고 다시 나머지 세 번째부터 4칸을 더 칠하여 총 6개의 칸을 색칠한다.) 했어요. 면: 설명 좀 해줄래?

혜: $\frac{3}{4}$칸에서 $\frac{3}{4}$의 $\frac{2}{5}$가 영호가 뛴 거리잖아요. $\frac{3}{4}$을 5랑 될 수 있게 15칸으로 나눠서 한 칸을 5개로 쪼개서 15칸을 하고 $\frac{2}{5}$니까 3배를 곱해서 6칸을 칠했어요.

면: 15칸에서 6칸? 그럼 영호가 뛴 거리는?

혜: 음... $\frac{6}{15}$

면: 그럼 그림에서 (15개로 나눈 것 중 하나를 가리키며) 이거 작은 한 칸은 얼마야?

혜: $\frac{1}{15}$이요...

면: 전체?

혜: 아! 전체에서는 $\frac{1}{20}$이요.

면: 그럼 색칠한 6칸은 전체 얼마야?

혜: 20칸으로 나눈 것 중에 6칸을 칠한 거니까 $\frac{6}{20}$ m요.

혜지는 15부분 중 6개를 색칠하였는데, 하나, 둘하고 손으로 두 개까지 집어가며 세더니 잠깐 멈추고 잠시 뒤 네 번째 칸까지의 분할 선을 진하게 그은 후 두 개까지 색칠하고 2초 후에 세 번째부터 여섯 번째까지 이어서 색칠하였다. 여기에서 $\frac{1}{4}$-단위에 5를 합성하여 2개의 칸을 택하고 전체가 $\frac{3}{4}$이므로 세 번 반복하여 2, 4, 6개의 칸을 색칠했다는 점이다. 혜지가 활동을 통해 전체를 작은 부분으로 분할하고, 분리, 반복의 조작을 순차적으로 거쳤지만, 합성 단위에 대한 등분할 조작만 구성한 학생이었다면 해결하기 어려웠을 ‘3의 $\frac{2}{5}$’의 문제 상황에 대하여 3부분($\frac{1}{4}$-단위로 이루어진 3개)을 단순히 5-단위로 합성만 한 것이 아니라 5가 3개씩 있는 15개로 변환할 수 있었다. 그리고 3부분 중 1부분에서 ‘부분의 양($\frac{2}{5}$)’을 택한 후 “3배를 곱해서 6칸을 칠했어요.”라는 설명으로부터 ‘부분의 양’을 분할하기만 하는 것이 아니라 부분의 양에 대한 ‘부분의 수’만큼 택할 수 있다는 인식은 분배 분할 조작을 사용하였다고 근거로 작용한다.

한편, 과제 [F5]는 ‘가분수의 가분수량’을 구하는 문제로 Hackenberg와 Tillema (2009)에서 제시된 5가지 유형의 과제 중 가장 어려운 유형이다. 이때 혜지는 1-단위에서 가분수인 1$\frac{11}{9}$은 나타낼 수 있었지만, 11의 $\frac{4}{3}$를 구하는 과정에서 ‘1분 40초’ 동안 아무 말이 없었고 허공에 손가락으로 무엇인가를 써보려는 행동만 취하였다. 이후에 면담자는 혜지에게 “1$\frac{11}{9}$은 $\frac{1}{9}$이 몇 개 있지?”라고 질문을 하였으며, 이에 혜지는 이미 자신이 그린 1$\frac{11}{9}$-막대 그림이 있음에도 불구하고, 그 아래 새로운 또 하나의 막대를 다시 그려 11부분 각각을 3개씩 나누기 시작하였다. 이 문제를 고민한 지 5분이 지난 후에야 비로소 혜지는 ‘$\frac{1}{11}$-막대에 대한 3-단위로의 합성’에 주목하게 된 것이다. 그리고는 33칸 중 11칸을 하나로 묶으며 이 문제가 제시된 후 처음으로 혜지는 웃음을 보였다. 이 과정에서 혜지는 3개씩 11부분인 동시에 11개씩 3부분으로 하여 1-3-33이면서 동시에 1-11-33으로의 두 개의 3수준 단위 구조로 -막대 그림을 바라볼 수 있게 된 것으로 판단된다.¹²

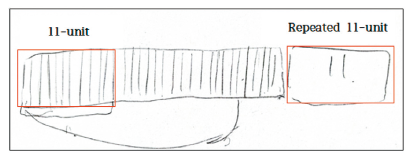
이후로 혜지는 Figure 7과 같이 11의 $\frac{4}{3}$를 구성하기 위해 1-3-33에서 3개씩 11부분을 11개씩 3부분인 1-11-33이라는 구조로 변환하여 ‘반복된 11-단위’와 같이 11을 하나 더 추가해 총 44칸의 막대 그림을 완성하였다. 그리고 이어진 면담자와의 대화이다.

면: 지금 그린 것을 값으로 나타내면 얼마가 될까?

혜: $\frac{44}{33}$이에요. 11칸에서 한 조각을 $\frac{1}{11}$을 세 조각을 냈어요.

면: $\frac{44}{33}$를 다르게 표현하면 얼마일까?

혜: $\frac{4}{3}$이요.

면: 영호가 뛴 거리는 $\frac{4}{3}$인가요?

혜: 아니요.

면: 1이 얼마지? 그림에서 1 m가 어디인지 표현해 볼래?

혜: 9개 칸까지 1 m에요.

면: 지금 44칸으로 나눈 이 그림에 다가 1 m가 어디쯤인지 나타낼 수 있니?

혜: 모르겠어요.

면: 한 칸을 3개씩 쪼개었지?

혜: (33칸의 마지막 칸부터 하나, 둘, 세더니 뒤에서 6번 째 칸에서 앞에 있는 첫 칸까지 곡선으로 묶어서 표시하고) 여기까지요.

면: 그럼 표시한 부분이 1인 거지?

혜: (응답이 없다.)

면: 1 m까지는 몇 칸이야?

혜: 33칸이요.

면: 그럼 지수는?

혜: 아... 아하! 27칸이요. (약 20초 이후) 음... (작은 목소리로) $\frac{44}{27}$요.

면: 아까 $\frac{44}{33}$는?

혜: 아까는 1 m로 한 것이 아니라... 지수가 뛴 거리로 해서 $\frac{44}{33}$이었던 것 같아요.

위의 대화에서처럼 혜지는 11부분 각각의 1($\frac{1}{9}$-막대)에 3-단위를 합성하였으나, 전체를 못 보고 11부분에 대한 $\frac{1}{33}$ - $\frac{33}{33}$ - $\frac{44}{33}$로의 3수준 단위 구조에 주목하였다. 즉, 가분수가 포함된 맥락에서는 활동을 통해 두 개의 3수준 단위 구조를 유지하는 것이 쉽지 않음을 보여 주었다. 결국 “1 m가 어디쯤인지 나타낼 수 있니?”, “1 m까지는 몇 칸이야?”와 같은 면담자의 추가 질문 이후에야 자신이 나타낸 막대 그림의 전체에 주목하는 듯하였으며, 전체 $\frac{27}{27}$로 회귀할 수 있었다.

분수 맥락에서 상연의 단위 조정

분수 맥락에서 상연의 단위 조정 앞서 세 가지 과제 [F1], [F2], [F3]을 모두 m × n직사각형 형태로 그리며 설명하였던 상연에게 과제 [F4]인 ‘$\frac{3}{4}$의 $\frac{2}{5}$’도 같은 문제 상황에서 물어봤다면 4 × 5 (혹은 5 × 4)의 직사각형을 그리며 여섯 칸을 색칠했을 것이다. 그러나 과제 [F4]는 앞서 세 가지 유형과는 문제 상황이 달랐다. 즉, 1 m를 기준으로 뛴 거리를 나타내는 문제 상황으로 상연에게 더 이상 직사각형으로 해결하기 어려운 문제였다. 상연은 혜지와 같이 1 m로부터 지수가 뛴 거리 $\frac{3}{4}$ m는 고민 없이 그림으로 나타낼 수 있었지만, 지수가 뛴 거리로부터 영호가 뛴 거리를 나타내는 과정에서는 시행착오를 거치게 된다. 다음은 과제가 주어진 후 이루어진 상연과의 대화 일부이다.

면: 그림은 선생님이 따로 주지 않았는데, 1 m 그림을 그려서 지수의 $\frac{3}{4}$을 나타내볼까요?

상: (직사각형 하나 그리고 이를 4등분한 다음 그중에서 세 부분을 색칠하며, 아래 “지수가 뛴 거리 $\frac{3}{4}$ m”라고 적는다.)

면: 그림에다가 영호가 뛴 거리를 나타내볼래?

상: (세 부분 중 한 부분을 절반으로 다시 나누다가 지운다.) 꼭 지수 그림에서 나타내야 하는 거죠?

면: 응.

상: (세 부분을 새롭게 나누기 시작한다.)

면: 지수의 한 칸을 나누고 있는 거야?

상: 네.

면: 어떻게 나누고 있어?

상: 지수의 전체를 5개로 나누고 있어요.

면: 지수가 원래 3개의 칸으로 나누어져 있었는데, 새롭게 나누는 거야?

상: 네. 눈대중으로요.

면: 지수의 3칸을 5개로 정확하게 나눌 수는 없을까?

상: 자를 대고요?

면: 그건 아니고...

상: (문제만 바라본다.)

면: 그럼 예를 들어 3조각의 케이크를 5명에서 나눠 먹으려고 한다면 자를 사용할 수도 없고, 어떻게 정확하게 나누어 먹을까? 어떻게 나눌 것 같아? 상: 음... 한 조각을 5개씩 나누면 될까요?

처음에 상연은 지수의 세 부분 중 한 부분($\frac{1}{4}$)을 절반으로 나누다가 바로 지우고는 ‘지수가 뛴 거리 전체’를 하나인 1-단위로 보고 5등분하였다. 이후에 “지수가 원래 3개의 칸으로 나누어져 있었는데, 새롭게 나누는 거야?”라고 면담자가 물어보자, “눈대중으로요.”라고 답하였다. 그리고 ‘3분 20초’가 지난 뒤 면담자의 추가 질문을 통해 비로소 상연은 “한 조각을 5개씩 나누면 될까요?”라고 답하며 3부분에 5단위를 합성하기 시작했다. Steffe (2003)에 의하면 $\frac{1}{3}$의 에 $\frac{1}{4}$대해 1을 3으로 분할하고, 3을 4로 분할하는 과정에서 합성 단위를 생성하여 전체를 1-3-12라는 3수준 단위 구조로 구성할 수 있을 때, 두 분할의 합성이 재귀적이라고 하였다. 면담 과정 중 상연의 “눈대중”이라는 표현에서 알 수 있듯이 상연은 단위분수의 진분수 곱셈에서는 두 분할의 합성이 재귀적이지 못한 것으로 보이며, 혜지가 스스로 단위를 합성하면서 보여주었던 시행착오들과 비교되는 모습이다. 다음은 지수가 뛴 거리의 $\frac{2}{15}$에 대한 상연과 면담자와의 대화 일부이다.

상: (15개 중에서 3개의 칸을 색칠하고 3초 뒤 네 번째 칸부터 다시 3개의 칸을 더 색칠한다.)

면: 선생님이 색깔 있는 펜을 빌려줄까?

상: 어! 네. (빨간색 볼펜으로 6개의 칸을 색칠한다.)

면: 몇 칸을 색칠했어?

상: 6개요.

면: 왜?

상: 이 중에서 $\frac{2}{5}$칸인데, 한 개를 $\frac{2}{5}$로.. $\frac{2}{15}$만큼인데, 얘가 한 칸에 5칸이니까 두 칸은 $\frac{2}{15}$니까, $\frac{2}{5}$에 $\frac{3}{1}$을 곱해서... (목소리가 들리지 않는다.) 5...

면: $\frac{2}{5}$에서 3을 곱해서?

상: (작은 목소리로) 잠깐만요... (활동지에 “$\frac{2}{5}$ × $\frac{3}{3}$= $\frac{6}{15}$”라고 쓴다.) 총 15칸이 되고, 색칠해야 되는 칸은 총 6칸이에요.

면: 지수의 색칠한 6칸은 얼마야?

상: $\frac{6}{15}$이요. $\frac{2}{5}$

면: 전체 1 m에서 영호가 뛴 거리는 얼마를 나타내는 것 같아요? 여기 전체 1 m에서..

상: 아! (막대 그림의 전체 20개를 빨간색 볼펜으로 묶으며) $\frac{6}{20}$이요.

면: 왜?

상: 왜냐하면 총 1이 아니라 총 $\frac{3}{4}$ m이니까 $\frac{1}{4}$만큼을 더 채워야 1 m가 되어서 그래서 여기가 $\frac{3}{4}$을 5칸씩 나누었을 때 색칠한 칸이니까 여기도 (1 m를 4등분한 것 중 지수가 뛴 거리 3칸 말고, 마지막 한 칸을 가리키며) 똑같이 5칸으로 나눠서 총 1 m의 20개 중 6개니까요.

상연은 3이 5로 나누어떨어지지 않기 때문에 3을 5라는 합성 단위의 반복으로 구성하는 것이 불가능하다는 것은 인식하고 있었다. 비록 분할에 대한 어려움을 보여 면담자가 활동 중에 추가 질문들을 했었지만, 상연은 ‘세 조각의 케이크를 5명이 나눠 먹는 상황’으로부터 전체 3이 5로 나누어떨어지도록 더 작은 부분으로 분할해야 한다는 아이디어와 연결시켜 합성 단위에 대한 등분할 조작의 가능성을 보여주었다. 이 과정에서 상연의 설명과 행동은 두 가지 측면에서 주목해 볼 수 있는데, 한 가지는 실제 막대 그림에서 분할의 여러 시행착오를 보여주며 ‘15개 중 $\frac{2}{5}$가 6개’임을 나타냈고, 조작 활동 중에서 일부를 반복하여 곱셈적 상황으로 순차적 접근을 하고 있다는 점이다. 다른 한 가지는 앞선 문제들과 같이 수치적 계산으로 문제의 답을 확인하고 설명을 이어가는 일관된 모습을 보여주었다는 것이다. 충분히 자신이 보여준 행동으로부터 분할의 과정을 통해 15의 $\frac{2}{5}$가 6임을 설명할 수 있었으나, 설명 전에 수치적 계산을 하여 답을 확인한 후에야 자신의 문제 해결 과정을 설명하였다. 이후 상연은 $\frac{15}{15}$-막대 그림으로 문제를 바라보며 자신이 답으로 택한 6이 $\frac{6}{15}$이라고 했지만, ‘전체 1 m’에 대한 면담자의 질문에 자신이 나타낸 막대 그림 보고, 전체를 펜으로 표시하며 5-단위 4개가 전체인 1($\frac{4}{4}$)로 회귀할 수 있었다.

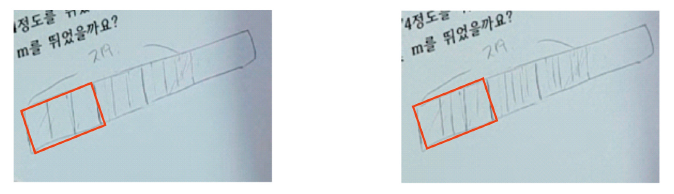
과제 [F5]에서 처음 1분 40초 동안 아무 응답이 없었던 혜지와는 달리, 상연은 ‘눈대중’으로 분할하였던 과제 [F4]와 같은 방법으로 아무런 고민 없이 바로 $\frac{11}{9}$에서 11부분을 눈대중으로 Figure 8과 같이 새롭게 4등분하였다. 다음은 상연의 눈대중으로 분할하는 과정에서의 설명이다.

상: (빨간색 볼펜으로 6번째 칸의 절반을 나누고, 세 번째와 네 번째 칸을 구분하는 선을 빨간색 볼펜으로 더 진하게 그은 다음, $\frac{8}{9}$지점과 $\frac{9}{9}$지점의 절반을 긋고, $\frac{11}{9}$인 지수가 뛴 거리에 이어서 지수가 뛴 거리의 $\frac{1}{4}$과 비슷한 크기의 사각형을 빨간색 볼펜으로 그린다. 그림 아래 “영호가 뛴 거리”라고 적는다.)

면: 어떻게 그렸는지 설명해줄래?

상: ($\frac{11}{9}$ 뒤에 빨간색 볼펜으로 이어서 그린 사각형을 3칸으로 나눈다.) 움... (1 m를 가리키며) 지수가 뛴 거리를 3칸으로 나누면... (그림 전체를 가리키며) 이게 총 영호의 $\frac{3}{4}$인거니까... 어! 근데 (지수가 뛴 거리를 가리키며) 여기가 4칸인데요?

면: 다시 그려야 할 것 같아?

상: 네. 다른 색으로 다시 그릴게요. (파란색 볼펜으로 펜을 바꾸어 역시 3개씩 묶어서 $\frac{11}{9}$을 또 아까처럼 네 칸으로 나누었다.)

면: 어? 잘 나눈 거 맞아? 다시 다른 색으로 표시해 볼까?

상: 세 칸으로 나눈 거니까.. (하늘색 형광펜으로 이번에는 4개씩 묶어서 한 칸을 만들고 두 번째, 세 번째 칸은 대충 나누어서 $\frac{11}{9}$이 4개씩 세 묶음이 되도록 표시한다.)

면: 이번에는 잘 나눈 거 맞아?

상: 네. 지수가 뛴 거리의 세 칸으로 나누고 하나를 더 늘렸어요. $\frac{4}{4}$중 3칸인 거니까... 영호가 뛴 거리는 지수의 $\frac{4}{3}$는 얘가 영호의 반대로 $\frac{3}{4}$인 거니까요. 영호가 뛴 거리만큼이 되니까 3칸으로 나누고 그 만큼 하나 더 늘렸어요.

면: 그럼 지수가 뛴 거리를 세 칸으로 나누었다고 했는데, 그 한 칸이 얼마를 나타내는 거야?

상: $\frac{11}{9}$의 $\frac{1}{3}$이요. (활동지에 “$\frac{11}{9}$×$\frac{1}{3}$ = $\frac{11}{27}$”이라고 적는다.)

면: 그런데 그림으로 $\frac{11}{27}$인지 확인할 수 있을까? 선생님은 잘 모르겠는데?

상: 아하... 여기서 약간 어.. (30초 후) 모르겠어요. 여기서 설명을 잘 못하겠어요.

상연은 11부분에 3-단위를 합성하기보다는 11부분을 새롭게 1-단위로 보고 3으로 나누고 싶었던 것 같았다. 그러나 3으로 나누지 않고 자신의 말과는 달리 4로 나누는 시행착오를 두 번이나 거친 후에 세 번째 시도에서 11부분을 1-단위로 보고 3으로 나누었다. 이 과정은 1에서 $\frac{11}{9}$을 나타내기 위한 방식과 유사하며, 11부분에서 가분수 $\frac{4}{3}$만큼을 그림으로 나타내기 위해 ‘3으로 나눈 양’을 네 번 반복한 것으로 보인다. 이때 ‘3으로 나눈 양’은 11부분 각각의 1에 3을 합성하여 구성한 양이 아니므로 Figure 6의 왼쪽 그림과 같이 상연에게는 ‘미지의 양’이다. 따라서 상연에게 $\frac{11}{9}$은 이전의 3수준 단위 구조인 $\frac{1}{9}$ - $\frac{9}{9}$ - $\frac{11}{9}$이 아니라 새로운 3수준 단위 구조 $\frac{1}{3}$ - $\frac{3}{3}$ - $\frac{4}{3}$에서의 새로운 1-단위($\frac{3}{3}$)이며, ‘미지의 양’을 구하기 위해서는 수치적 계산이 필연적이었을 것으로 판단된다 결국 상연은 수치적 계산 결과에 대한 양적 의미를 자신이 그린 그림과 연결 지어 설명하지 못하였고, ‘30초’라는 긴 시간 동안 고민하다가 “여기서 설명을 잘 못하겠어요.”라며 면담을 마무리하였다.

두 학생의 비례 문제 해결 과정에서 나타나는 분수 지식

혜지의 비례 문제 해결 과정

과제 [P1]에서 [P2]의 3번 문제까지는 막대 그림이 제시되지 않은 비례 문제로 혜지는 비를 하나의 묶음으로 자연수 배수 관계를 이용하여 해결하였다. 특히 자연수 배수 관계가 아닌 문제 상황에서는 한 단위와 그에 대응하는 다른 한 양의 결합된 비 개념을 이용하여 곱셈적으로 문제를 해결하였다. 문제 해결 과정을 구체적으로 살펴보면, 과제 [P1]은 우유 4컵에 초코파우더 3스푼인 ‘4대3’의 비가 성립하는 문제 상황에서 우유 7컵에 대한 초코파우더의 양을 물어보는 문제이다. 혜지는 자연수 배수 관계가 성립하지 않자 ‘50초’라는 시간 동안 무언가를 고민하는 듯하였다. 그리고 활동지에 “3×$\frac{1}{4}$ = $\frac{3}{4}$”라고 적었으며, 이에 대한 설명으로 “4컵에 3스푼이니까 한 컵에 넣는 스푼은 $\frac{3}{4}$스푼이고, 7컵이 되려면 3컵이 더 필요하니까 우유 3컵이면 초코파우더가 $\frac{9}{4}$스푼, 7컵이면 3스푼에 2$\frac{1}{4}$스푼을 더해서 5$\frac{1}{4}$스푼이에요.”라고 하였다. 이와 같은 반응은 Johnson (2015), Lee와 Lee (2020)에서의 내재화된 비인 ‘하나당으로의 비’ 개념에서 ‘우유 한 컵당에 대응하는 초코파우더의 양 $\frac{3}{4}$에 대한 결합된 비’로 해석된다. 즉, 우유 3컵에 대한 미지의 초코파우더 양을 구하기 위해 4:3의 비로부터 우유 1컵에 대한 미지의 초코파우더의 양인 $\frac{3}{4}$을 찾을 수 있었다. 과제 [P2]의 물 5컵에 레몬 시럽 2컵으로 하는 ‘5대2’ 문제 상황에서도 자연수 배수 관계를 이용하여 2번 문제 ‘물 75컵에 대한 레몬 시럽의 양’을 쉽게 답하였다. 또 3번 문제인 레몬주스 전체 양 140컵을 만들기 위해 물과 레몬 시럽의 양을 각각 물어보았을 때에는 ‘5대2’라는 비를 하나의 묶음으로 하여 “물과 레몬 시럽이 총 7컵이니까 7이 140이 되려면 20을 곱하면 되잖아요. 그래서 물 5컵에 20을 레몬 시럽 2컵에 20을 곱했어요.”라고 설명하였다. 즉, 전체 양 140컵을 미지의 합성 단위 7개로 이루어진 3수준 단위 구조로 보고 140-단위를 7부분으로 등분할하여 미지의 합성 단위의 크기를 찾아낼 수 있었다.

한편, 과제 [P2]에서 막대 그림이 제시된 4번 문제는 물과 레몬 시럽이 ‘5대2’의 비를 만족할 때, 레몬주스 210컵을 만들기 위한 물과 레몬 시럽의 양을 구하는 문제이다. 이때 혜지는 바로 “물 150컵, 시럽 60컵”으로 답하였으나 그림을 어떻게 나타내야 할지 어려워하였다. 면담자는 주어진 막대 그림이 꼭 물 5컵과 레몬 시럽 2컵을 의미하는 것은 아니라고 하였고, 혜지는 “150 나누기 5면 30이니까, 60에서 나누기 5를 하면 30이 나왔어요.”라며 막대 그림의 각 칸에 모두 “30”이라고 적었다.

다음 [P2]의 5번 문제로 ‘물 21컵에 대한 레몬 시럽의 양’을 물어보는 상황에 혜지는 ‘3분 28초’ 동안 아무 말을 하지 않고 문제만 바라보았다. 이후 활동지의 막대 그림 아래 “21×$\frac{1}{5}$ = 2$\frac{1}{5}$”라고 적은 뒤, Figure 9와 같이 물 5-막대의 첫 번째 칸과 두 번째 칸에 각각 “4$\frac{1}{5}$”라고 적었고, 레몬 시럽 2-막대 아래 “8$\frac{2}{5}$”라고 적었다.

설명을 요구하는 면담자의 질문에 혜지는 “물 21컵에 하니까, 여기 (물 5-막대를 가리키며) 한 칸당 몇 컵을 넣어야 할지를 구해서 21×$\frac{1}{5}$하면 4$\frac{1}{5}$컵이 나오고, 5배를 하면 21컵이 나와서 한 칸당 4$\frac{1}{5}$을 하고, 그러면 레몬 시럽이 8$\frac{2}{5}$컵이 나와요.”라고 설명하였다. 혜지는 물 21컵을 물에 해당하는 비인 5(즉, 5부분)로 보고 1부분을 구하기 위해 21을 5로 나누었으며, 2부분에 해당하는 레몬 시럽의 양을 구하기 위해 1부분에 해당하는 양(2$\frac{1}{5}$)에 2를 곱하는 (혹은 2$\frac{1}{5}$을 두 번 반복하여 더하는) 문제 상황으로 인식한 것이다. 이때 주목할 점은 혜지가 물 5-막대에 대하여 별도로 분할하는 활동을 보이지 않은 상태에서 물 21의 단일 단위(4$\frac{1}{5}$컵) 각각에 대한 5부분으로 인식하고 있으므로 이를 분배하는 방식으로 레몬 시럽의 양을 구했다는 점이다. 이는 앞서 ‘$\frac{3}{4}$의 $\frac{2}{5}$’의 분수 과제에서 ‘3의 $\frac{2}{5}$’에 대한 문제 해결 과정 중 (3부분에서) 1부분의 양 $\frac{2}{5}$에서 부분의 수 3만큼 택할 수 있다는 아이디어와 21로부터 부분의 양인 단일 단위 4$\frac{1}{5}$을 부분의 수 2(레몬 시럽 2-막대)만큼 택할 수 있었던 조작과 유사한 활동이라고 할 수 있다.

막대 그림이 제시되지 않았던 과제와 비교해 볼 때, 초코우유 문제에서 혜지는 우유 한 컵에 대한 초코파우더의 양을 반복하여 우유 7컵에 대한 초코파우더의 양을 구했다. 반면 막대 그림이 제시된 과제에서는 막대 그림 전체 21컵을 1-단위로 두고, 5로 나누어 2$\frac{1}{5}$의 단일 단위인 부분의 양을 레몬 시럽 3-막대 각각에 분배하는 방식(즉, 부분의 수만큼 택하는 방식)으로의 곱셈적 상황으로 보았고, 그 과정에서 초코우유 문제 해결을 위한 시간보다 ‘4배’의 시간이 필요했던 것으로 보인다. 혜지에게 ‘4배’라는 시간은 비례 문제를 막대 그림으로 나타내는 과정이 익숙하지 않아서였을지 모르지만, 막대 그림으로 인하여 주어진 문제 상황에 대한 접근 방식의 전환이 필요했기 때문으로도 해석된다.

상연의 비례 문제 해결 과정

상연의 비례 문제 해결 과정을 살펴보면 과제 [P1]의 자연수 배수 관계가 성립되지 않는 문제 상황에서 혜지와 같이 당황해하는 모습을 보였다. 그러나 한 단위와 그에 대응하는 다른 한 양의 결합된 비 개념으로 접근했던 혜지와는 달리 ‘외항의 곱은 내항의 곱과 같다’라는 비례식 알고리즘을 사용하여 답을 구하였다. 이후로도 제시된 비례 문제들은 모두 비례식 알고리즘만을 이용해서 답을 구하였다. 상연이 구한 답에 대하여 면담자가 추가 설명을 요구하였을 때에도 비례식 알고리즘만을 반복하며, 다른 시도를 보이지 않았으므로 면담을 마무리하였다. 다음은 그로부터 4주 뒤에 진행된 추가 면담에서의 상연과 면담자의 대화 일부이다.

면: 물 5컵에 레몬 시럽 2컵으로 하는 레몬에이드를 만든다고 한다면 같은 맛을 내기 위해 물 7컵에는 레몬 시럽 몇 컵을 넣어야 할까?

상: (1분 동안 문제만 바라본다.) 약간.. 막히는 거 같은데요. (말끝을 흐린다.) 어려워요.

면: 왜?

상: 식을 정렬해서 해야되는데, 그게 잘 안 돼서요.

면: 어떻게 해야 할지 모르겠어?

상: 네.

면: 만약 물이 5컵의 절반이라면 시럽은?

상: (활동지를 바라만 본다. 문제를 읽은 지 ‘1분 50초’ 후 활동지에 적기 시작한다.) 시럽도 $\frac{5}{2}$... 한 컵이요. (활동지 문제에 ‘5대 2의 비’라는 표현에 밑줄을 긋고, “$\frac{5}{5}$대$\frac{2}{5}$”라고 고친 뒤 $\frac{2}{5}$에 7을 곱하여 $\frac{14}{5}$를 적는다.) 2.8컵이요.

면: 어떻게 나왔어?

상: $\frac{5}{5}$컵당 $\frac{2}{5}$컵. 그러니까 1컵당 $\frac{2}{5}$컵이니까 7을 똑같이 곱해서 $\frac{14}{5}$에요.

상연은 처음에 문제만 바라보며 1분 동안 아무런 시도조차 하지 못하더니 “식을 정렬해서 해야되는데, 그게 잘 안 돼서요.”라며 이전 면담에서 보여주었던 비례식 알고리즘에 의한 문제 해결 과정은 기억하지 못하는 듯하였다. 설명 전에 수치적 계산을 통해 먼저 답을 확인하던 상연의 이전 모습을 비춰보면 ‘식을 정렬한다’는 의미는 비례식 알고리즘의 수치적 계산을 의미했던 것으로 해석된다. 그리고 비례 문제에 대한 이전의 면담에서 상연이 사용했던 ‘비례식 알고리즘’은 양적 조작이 함께 수반되지 못한 수치적 조작에 불과했던 것으로 보인다.

어떻게 해야 할지 모르는 상연에게 면담자는 물 5컵이 아닌 5컵의 ‘절반’일 때 시럽의 양을 물어보았고, 이후로 상연이 활동지에 무언가를 적기 시작한 것은 과제가 주어진 지 ‘3분 10초’만이었다. 물이 $\frac{5}{2}$컵이면 레몬 시럽이 1컵이라는 사실로부터 상연은 물 5컵을 5로 나누어 물 $\frac{5}{5}$컵에 대한 시럽 $\frac{2}{5}$컵에 주목하였다. 상연은 물과 시럽의 비 ‘5대2’에서 물 한 컵에 대한 시럽의 양을 계산하기 위해 ‘$\frac{2}{5}$’이라는 양을 구성하기까지 ‘1분 50초’의 시간이 소요 더 필요했으며, 문제가 제시된 후부터 ‘3분 10초’라는 긴 시간은 상연이 ‘5대2’의 비에서 1에 해당하는 양을 구성하는 문제로 인식하는데 필요한 시간이었으리라 추측해 볼 수 있다.

다음 과제는 별도의 막대 그림이 제시된 ‘5대3’의 비례 상황에서 상연에게 레몬 시럽 5컵에 대한 물의 양을 물어보았다. 이때 상연은 Figure 10과 같이 레몬 시럽 3-막대 그림을 5개 부분으로 대충 나누었으며, 나눈 1부분의 크기와 비슷한 크기로 물 5-막대 그림을 8개로 나누고는 “8컵”이라고 답하였다. 이는 분수가 포함된 문제에서 일관되게 보여주었던 “눈대중”으로 분할했던 모습과 유사하다.

상연이 눈대중으로 막대를 분할했던 모습은 이전 면담에서 비례식 알고리즘만을 이용해서 답을 구한 뒤, 그림과 연결해서 설명하지 못하고 다른 시도조차 하지 않았던 모습과는 분명히 다른 모습이었다. 또한 막대 그림이 제시되지 않았을 때, 주어진 비로부터 1에 해당하는 양으로 해결했던 직전 문제에서의 해결 방식과도 다른 모습이었다. 상연은 눈대중으로 나눈 분할 선을 응시하며, 8컵이라고 답한 뒤에 생각에 잠긴듯하더니 “이게 정확하게 딱 나눠지는 것 같지가 않은데요.”라고 하였다. 여기서 면담자는 “아까 1번 문제도 딱 떨어지는 문제는 아니었는데?”라고 답하자, 면담자의 답변 이후 상연이 보여준 행동은 자신이 눈대중으로 분할했던 선을 지우는 행동이었다. “딱 나눠지는”이라는 말과 ‘선을 지우는’ 행동으로부터 상연은 한 단위에 다른 단위에 대한 합성의 필요성을 인식한 것으로 보인다. 이는 혜지의 문제 해결 과정과도 구별되는데, 만약 혜지가 이 문제를 해결했다면 레몬 시럽 5컵을 1-단위로 보고 분할 활동 없이 바로 $\frac{5}{3}$이라고 표현했을지 모른다. 그러나 상연은 눈대중으로 나누었던 분할 선을 지우며, 레몬 시럽 3-막대를 각 1로 구성된 세 부분으로 보고 1을 분할하는 모습을 보여준다. 처음에는 레몬 시럽 3-막대 그림의 각각의 칸들을 모두 절반씩을 나누어 총 6개 부분으로 나누더니 잠시 뒤 지우고, 다시 나누기 시작한다. 다음은 막대 그림을 분할하는 상연의 모습과 이어지는 면담자와의 대화 일부이다.

상: (활동지에 분할한 선을 지운다. 그리고 시럽 3칸을 절반씩 나누더니 잠시 뒤 지운다. 10초 뒤 시럽 3칸 각각을 5로 나누어 시럽 3-막대를 15개로 분할한 뒤, 물 5칸 각각을 시럽과 같이 5로 분할한다.)

면: 어허? 갑자기 5개씩 나누었네?

상: 네. (물과 시럽을 각각 5개씩 나눈 뒤 시럽 3-막대를 가리키며) 한 개당 5개면 3개니까 15개에요. 그리고 이걸 딱 3으로 나누면... (잠시 고민하다 시럽 15개의 칸을 3개씩 묶는다.)

면: 왜 3개씩 나누었어?

상: 5개가 되니까요.

면: 5개?

상: 5컵이요. 시럽을 15개로 만들면 15개니까 $\frac{15}{3}$은 5컵이에요. (물 5칸을 가리키며) 얘도 5개씩 나눠서 구하면 25개에요. (물의 막대 그림의 25개를 3개씩 묶는다.) 25도 딱 3으로 나누면 8과...

면: 하나가 남았네?

상: 8과 $\frac{1}{3}$이요. 아! 네. $\frac{25}{3}$컵이에요.

면: (시럽 3-막대의 15개 중 한 부분을 가리키며) 이 한 칸은 얼마야?

상: $\frac{1}{3}$이요.

면: $\frac{1}{3}$?

상: 아니, $\frac{1}{5}$? 원래 있던 그림이 3칸인데 이것을 다시 나눠서 15개를 3개씩 묶으면 5개가 되니까요. 아하! 3개 중 하나니까요. $\frac{1}{3}$이네요.

상연은 레몬 시럽 3-막대에 5를 합성하여 15부분으로 분할한 뒤에 3-막대를 15부분으로 동시에 물 5-막대에도 레몬 시럽과 같이 5를 합성하여 물 25부분으로 보았다. 이때 곧바로 레몬 시럽 3-막대를 5로 분할하지 못하였고, 여러 번의 시행착오를 거쳤으며 Figure 11과 같이 레몬 시럽 3-막대를 15부분으로 물 5-막대를 25부분으로 구성하며 ‘5대3’의 비례 관계를 ‘25부분 대 15부분’으로 보았고, 자연수 맥락에서 5씩 3개의 묶음인 15부분을 3씩 5개 묶음인 문제 상황을 인식하였다. 3수준 단위인 1-5-15를 1-3-15로 전환하는 과정에서 “이걸 딱 3으로 나누면...” 이라 말하고, ‘잠시 고민한 뒤에 3개씩 묶었다’는 점에 주목해 볼 필요가 있다. 자신이 구성한 3수준 단위를 자신이 나타낸 그림으로부터 이해하고 있으며 묶는 활동을 통하여 레몬 시럽 3컵을 5컵으로, 물의 양도 5-막대 25부분을 3개씩 묶어가며 8$\frac{1}{3}$컵임을 구하였다. 이러한 과정에서 보여지는 상연의 비례 문제에 대한 접근 방식은 시행착오를 거쳐서 진행된 분할로부터 자연수 맥락으로의 문제 상황으로 전환하여 순차적으로 수행된 조작 과정을 통해 ‘합성 단위에 대한 등분할 조작’ 방식으로의 문제 해결을 보여준 것으로 판단된다.

두 학생의 ‘닮은 도형’ 문제에서의 비교

다음은 과제 [P3]의 비례 개념이 포함된 닮은 도형 문제 상황으로 두 학생의 ‘휴대폰 속 사진의 확대, 축소’ 문제를 해결 과정을 비교해보고자 한다. 가로 5, 세로 3인 직사각형이 세로가 5일 때 가로의 길이를 구하는 문제에서 다른 비례 문제에서와 같이 결과만 보면 상연과 혜지의 문제 해결의 과정은 매우 유사한 모습이다. 두 학생 모두 활동지에 “$\frac{5}{3}$×5 = $\frac{25}{3}$”라는 식을 쓰며 가로의 길이가 $\frac{25}{3}$라고 답하였다. 그러나 문제 해결 과정에서 닮은 도형의 가로와 세로를 바라보는 접근 방식에 있어서는 앞서 비례 문제를 해결 과정에서 나타난 특성과 비교할 때 서로 다른 접근 방식을 보여준다. 두 학생의 문제 해결 과정 사이에는 미묘한 차이를 식별할 수 있는데, 혜지는 과제가 주어졌을 때 활동지에 “$\frac{5}{3}$×5 = $\frac{25}{3}$”라는 식을 쓰기까지 ‘45초’라는 시간 걸렸다. 다음은 혜지의 닮은 도형 문제에서의 면담자와의 대화 일부이다.

혜: (4초 후, 활동지에 식을 쓰기 시작한다. 활동지에 “$\frac{5}{3}$×5 = 3”을 쓰고 바로 지운다.) 음... (45초 후, 활동지에 “5×$\frac{1}{3}$ $\frac{5}{3}$×5 = $\frac{25}{3}$”을 적는다.) 했어요.

면: 얼마가 나왔어?

혜: 8$\frac{1}{3}$이요.

면: 왜?

혜: 세로의 길이 3에서 5가 되었으니까 이제 1만큼 늘렸으면 5 곱하기 $\frac{1}{3}$해서 $\frac{5}{3}$가 늘어났다고 했거든요.

면: 세로가 1일 때 가로가 $\frac{5}{3}$이라는 말이야?

혜: 아니요. 어... 그러니까... (말끝을 흐린다.)

면: $\frac{5}{3}$가 뭐지?

혜: 그러니까 이게... (처음 직사각형을 가리키며) 여기 직사각형에서 원래 길이 1이 (확대한 직사각형을 가리키며) 여기서는 $\frac{5}{3}$칸이 늘어난 것이고, 그래서 세로가 5라면.. $\frac{5}{3}$가 3개면 5가 나오잖아요. 그래서 $\frac{5}{3}$가 5개니까 5 곱하기 $\frac{5}{3}$해서 $\frac{25}{3}$가 나왔어요.

면: 아하! 그렇구나! 그럼 1일 때 $\frac{5}{3}$칸인 것은 어떻게 알았어?

혜: 음... 이게 3으로 작은 게 3으로 늘렸을 때 세로가 5만큼 된 거니까, 원래 3중에 1이 얼마를 의미하는지 구하기 위해서 5 곱하기 $\frac{1}{3}$을 하면 5중의 $\frac{1}{3}$이 $\frac{5}{3}$칸이니까요. 그래서 원래의 길이 3중의 1이 $\frac{5}{3}$라는 것을 구했어요.

45초 후에 혜지가 활동지에 적었던 식 “5×$\frac{1}{3}$, $\frac{5}{3}$×5 = $\frac{25}{3}$”과 이어지는 대화에서 혜지가 구성한 $\frac{5}{3}$이라는 양은 세로가 1일 때의 가로의 길이와는 차이가 있다. 혜지는 $\frac{5}{3}$에 대한 설명으로 세로의 길이 1이 “3중의 1이 얼마를 의미하는지 구하기 위해서”라는 말처럼 세로 3인 길이를 5로 만들기 위해 세로를 3-막대 그림으로 보고 5를 3으로 균등하게 나누어 3-막대의 세 부분 중 한 부분의 양으로 $\frac{5}{3}$를 인식하였다. 이에 대한 근거로는 혜지가 $\frac{5}{3}$이라는 양을 구성하고 “세로가 5라면..” 이후에 $\frac{5}{3}$에 바로 5를 곱하는 것으로 설명하지 않았다는 사실이다. ‘원래 직사각형’ 세로의 길이 1에 대한 ‘확대한 직사각형’ 세로의 길이 $\frac{5}{3}$를 생각했다면 곧바로 $\frac{5}{3}$에 5를 곱해서 $\frac{25}{3}$를 답했을 것이다. 그러나 혜지는 “세로가 5라면.. $\frac{5}{3}$가 3개면 5가 나오잖아요. 그래서 $\frac{5}{3}$가 5개니까”에서와 같이 가 3개 있을 때 세로가 5라고 하여 $\frac{5}{3}$를 세로 3-막대와 가로 5-막대에 들어갈 각각의 단일 단위로 인식한 것이며, 단일 단위 $\frac{5}{3}$를 세로 3-막대와 가로 5-막대로 분배하는 방식으로 해석된다. 그리고 이 과정에서 미지의 가로의 길이를 구하기 위해 세로의 길이 5를 3부분으로 나누고, 부분의 양 $\frac{5}{3}$를 가로 대 세로의 길이 비 5:3으로부터 부분의 수 5만큼 택하는 방식의 곱셈적 상황으로 보았다.

한편, 문제 해결 과정이 오랜 걸렸던 혜지와 달리 상연은 Figure 12와 같이 세로와 가로의 길이에 대한 표를 만들어 세로 3, 가로 5에서 2배, 3배, 4배의 자연수 배수 관계인 덧셈적으로 수들을 나열하였다. 그리고 세로 3을 3으로 나눈 뒤에 “분수로 만들면 $\frac{3}{3}$은 1이고, 그럼 가로는 $\frac{5}{3}$이니까요.”라고 하며 세로 1에 대한 가로 $\frac{5}{3}$를 구하였다. 이를 통해 “1씩 세로가 늘어난다면 1, 2, 3, 4, 5니까 가로도 $\frac{5}{3}$에 5를 곱하면 $\frac{25}{3}$이에요.”라고 답하였다.

상: 아니, $\frac{1}{5}$? 원래 있던 그림이 3칸인데 이것을 다시 나눠서 15개를 3개씩 묶으면 5개가 되니까요. 아하! 3개 중 하나니까요. $\frac{1}{3}$이네요.

상연은 막대 그림이 제시되지 않았던 비례 문제에서의 해결 과정과 같이 ‘세로 대 가로’를 ‘3대5’의 비에서 ‘1에 해당하는 양’을 구성하는 문제로 인식하며 문제를 해결하였던 것이다. 직전에 주어졌던 ‘막대 그림이 제시된’ 레몬주스 문제와 동일한 문제로 보고, 닮은 도형 문제 상황을 막대 그림이 제시되었을 때로 재구성하는데 ‘45초’라는 시간이 필요했던 혜지와 달리, 상연은 ‘막대 그림이 제시되지 않았던’ 비례 문제로 보고 한 단위와 그에 대응하는 다른 한 양의 결합된 비 개념인 ‘1에 해당하는 양’을 구성하는 문제로의 인식이 문제 해결에서 중요하게 작용한 것으로 보여진다.

결론 및 제언

본 연구는 비례 문제 해결 과정에서 분수 지식이 어떻게 관련되는지를 확인해 보고자 하였다. 이를 위해 자연수 맥락에서는 단위 조정 3단계로 판단되었으나, 가분수가 포함된 분수 맥락에서는 ‘활동을 통해’ 3수준 단위 조정이 가능했던 학생들을 대상으로 나타나는 분할 조작과 단위 조정 활동이 비례 문제 해결 과정에서 어떠한 관련성을 가지는지 살펴보았다. 본 연구의 결과를 정리해보면 다음과 같다.

첫째, 자연수 맥락에서 단위 조정 3단계 학생으로 보여지는 두 학생은 분수의 곱셈 상황에서 활동을 통해 3수준 단위를 조정하는 모습을 보여주었으며, 활동을 통해 3수준 단위를 조정하는 두 학생 간에는 같은 단위 조정 수준 안에서 식별할 수 있는 차이점이 있었다. ‘진분수의 진분수’와 관련된 분수의 곱셈에서 두 학생은 모두 단위의 단위를 바로 합성하지 못하고 분할 과정에서 시행착오를 거쳤으며, 전체가 아닌 부분의 양을 1로 보고 면담자의 추가 질문과 자신이 나타낸 분할 그림을 다시 확인하고서야 비로소 ‘전체에 대한 부분의 양’으로 회귀가 가능한 공통적인 모습을 보였다. 반면, 단위의 단위에 대한 합성으로부터 부분의 양을 택할 때, 혜지는 부분 중의 하나를 분리하여 각 부분에서 취할 수 있는 양으로 접근하였다면, 상연은 수치적 계산에 의존하며 자신이 구한 답을 그림으로부터 확인한 이후에야 설명하는 모습을 보였다.

한편, 두 학생 모두 1-단위로부터 가분수에 대한 구성이 가능한 것으로 보였으나, 가분수가 포함된 분수의 곱셈 상황에서는 분할 조작에 있어서 여러 번의 시행착오를 거쳤다. 그러나 혜지는 초기에 분할 과정에서 시행착오를 거치기는 했지만, 분할을 지속적으로 시도해 나아가는 과정에서 두 분할의 합성으로 합성 단위를 생성하여 전체를 3수준 단위 구조로 볼 수 있었다. 그리고 자신이 나타낸 막대 그림으로부터 부분의 부분과 전체 사이의 관계를 바라보았다. 특히 혜지는 가분수가 포함된 분수의 곱셈 상황에서 합성 단위에 대한 스플리팅 조작으로 두 개의 3수준 단위 구조 사이의 전환하는 모습도 보여주었다. 반면 일관되게 ‘눈대중’으로 분할하는 모습을 보이며 면담자의 질문과 개입에도 불구하고 진분수의 곱셈에서 재귀 분할이 쉽게 발현되지 못했던 상연은 가분수가 포함된 분수의 곱셈에서도 합성 단위의 구성에 어려움을 보였고, 결국 부분의 부분에서 전체와의 곱셈적 관계에 주목하지 못하였다. 상연이 분할과 관련된 문제를 학교에서 다루어 보지 않았기 때문일 수도 있지만, 약 두 달 정도 진행된 면담 과정에서 제시된 과제와 유도되는 활동들은 대부분 분할과 관련이 되었음을 감안해 볼 때 상연의 ‘눈대중’ 분할은 지속적으로 나타났던 모습이다. 이러한 모습은 자신이 이전에 구성한 3수준 단위 구조에서 나타난 결과를 다시 1-단위로 하여 새로운 3수준 단위 구조를 만드는 과정에서 이전의 분할선을 무시하고 새롭게 나누는 모습으로 하나의 3수준 단위에서 또 다른 3수준 단위 사이의 구조적 전환이 유연하게 이루어지지 못하고 있다는 근거로 해석된다. 이러한 두 개의 3수준 단위 사이의 구조적 전환의 어려움은 재귀적이지 못한 두 분할의 합성으로부터 가분수가 포함된 분수의 곱셈 상황에서 재귀 분할이 내재화되지 못한 것으로 판단된다. 따라서 분수 곱셈 상황에서 상연은 수치적 조작에 의존하며, 양적 조작의 의미가 수치적 조작과 함께 문제 해결 과정에 수반되지 못한 것으로 보인다. 이에 Hackenberg와 Tillema (2009)에서 재귀 분할을 일반적인 조작 방식으로 추상화한 학생은 분수의 곱셈 상황에서 두 분수 사이의 조작을 보다 의미 있게 수행할 수 있도록 한다는 사실은 고무적이다.

이와 같이 자연수 맥락에서는 단위 조정 3단계 학생으로 같은 수준의 단위 조정 단계에 있다 하더라도 다양한 분수의 곱셈 상황에서는 조작 방식의 차이를 보이며 문제 상황에서 생성되는 단위 구조의 복잡성에 따라 서로 다른 양적 조작 방식을 보여주었다.

둘째, 두 학생의 비례 문제 해결에서는 그 결과만 보면 유사하다고 볼 수 있으나, 접근하는 방식에 있어서 식별되는 차이를 보였다. 그리고 분수의 곱셈 문제 상황에서 보여주었던 분할 조작과 단위 조정 과정에서의 양적 조작 방식의 차이가 두 학생의 비례 문제 접근 방식에서 보여준 식별되는 차이와 관련성을 가지는 것으로 판단된다. 막대 그림이 과제에 제시되지 않았을 때, 두 학생은 모두 비를 하나의 묶음으로 하여 자연수 배수 관계로 해결하였다. 자연수 배수 관계가 성립되지 않은 문제 상황에서도 두 학생 간의 정도의 차이는 있었지만, 결과적으로 한 단위와 그에 대응하는 다른 한 양의 결합된 비 개념인 ‘1에 해당하는 양’을 구성하여 곱셈적으로 문제를 해결하였다. 그러나 막대 그림이 과제에 제시되었을 때, 두 학생은 각각 다른 문제 상황으로 인식하며 서로 다른 방식으로 문제에 접근하는 모습을 보였다.

우선 분수 맥락에서 분할의 시행착오를 거치며 활동을 통해 두 분할의 합성으로 합성 단위를 생성하여 전체를 3수준 단위 구조로 볼 수 있었던 혜지는 막대 그림이 주어진 비례 문제에서는 이전과는 다르게 ‘1에 해당하는 양’에 주목하지 않았다. 물론 물과 레몬 시럽이 ‘5대2’의 비를 만족할 때, 물 21컵에 대한 레몬 시럽의 양을 물어보는 상황에서 혜지는 막대 그림으로 문제 상황을 이해하기 위해서 ‘3분 28초’라는 긴 시간이 필요했지만, 물 1컵에 대한 레몬 시럽의 양으로 접근하지 않았다. 물 21컵을 5부분으로 인식하여 5부분 중 1부분을 구하기 위해 21을 5로 나누어 단일 단위 2$\frac{1}{5}$을 구성하였다. 그리고 2부분에 해당하는 레몬 시럽의 양을 구하기 위해 단일 단위로부터 부분의 수를 두 번 택하는 문제 상황으로 보았다. Shin과 Lee (2019)에 의하면 합성 단위에 대한 스플리팅 조작이 이와 같은 단일 단위에 대한 구성을 가능하게 한다고 보았는데, 혜지가 문제 해결 과정에서 직접 막대 그림을 분할하지 않고도 측정 가능한 양(단일 단위의 구성)으로 인식할 수 있었던 것은 합성 단위에 대한 스플리팅 조작의 가능성과도 연결시켜 볼 수 있는 부분이다. 또 앞서 분수의 곱셈 문제 ‘$\frac{3}{4}$의 $\frac{2}{15}$’를 ‘3의 $\frac{2}{15}$’로 보고 해결 과정에서 (3부분 중) 1부분의 양 $\frac{2}{15}$에서 부분의 수 3만큼 택할 수 있다는 아이디어와도 에유사한 조작 활동으로 자신이 구성한 단일 단위를 각 부분으로 분배하는 방식을 보여주었다. 이러한 접근 방식은 비례 개념이 포함된 ‘닮은 도형’ 문제에서도 나타나는데, 가로와 세로의 비가 일정한 직사각형에서 세로 1에 대한 가로의 길이가 아닌 가로와 세로 각각의 서로 다른 양적 구조 사이에 하나의 단일 단위를 구성하여 구성된 단일 단위를 분배하는 방식으로 닮음비에 접근하였다. 이는 두 개의 3수준 단위 사이의 구조적 전환의 어려움을 보여주며 재귀적이지 못한 두 분할의 합성으로부터 가분수가 포함된 분수의 곱셈 상황에서 재귀 분할이 내재화되지 못한 것으로 판단되는 상연에게서는 발견할 수 없었던 구별되는 지점이다.

비례 개념이 포함된 ‘닮은 도형’ 문제에서 상연은 막대 그림이 주어지지 않았을 때와 같이 직사각형의 가로와 세로에 대한 비(두 외연량의 비)에서 하나의 외연량인 세로의 길이를 1로 하고, 세로의 길이 1에 대응하는 다른 외연량인 가로의 길이를 통해 닮음비로 확장하였다. 한편 막대 그림이 주어진 비례 문제에서는 닮은 도형 문제와 같이 ‘1에 해당하는 양’으로 접근하지는 않았지만, 물과 레몬 시럽이 ‘5대3’의 비를 만족할 때, 레몬 시럽 5컵에 대한 물의 양을 물어보는 상황에서 상연은 이전의 분수 맥락에서 일관되게 보여주었던 “눈대중” 분할의 모습을 보이며 여러 번의 시행착오를 거쳤다. 그리고 결과적으로 물 5-막대와 레몬 시럽 3-막대 그림에서 5를 합성하여 물 25부분과 레몬 시럽 15부분으로의 문제 상황으로 인식하였다. 막대 그림이 주어지지 않았을 때처럼 레몬 시럽 1컵에 대한 물의 양 $\frac{5}{3}$컵으로도 생각해 볼 수도 있었으나, 가분수가 포함된 분수의 곱셈 문제에서 막대 그림으로부터 합성 단위에 대한 구성을 어려워했던 상연은 물과 시럽 각각에 5를 합성하여 물 25부분과 레몬 시럽 15부분의 문제 상황으로 전환한 것이다. 레몬 시럽 15부분을 3개씩 묶어 5컵이 되는 것으로부터 물 25부분이 3개씩 묶어 8컵하고 1부분이 남는 것으로 이해하였다. 남은 1부분이 도중에 $\frac{1}{3}$인지, $\frac{1}{5}$인지 혼란스러워했지만, 자신이 나타낸 그림으로부터 확인할 수 있었다. 즉, 상연은 자연수 맥락으로의 문제 상황으로 전환하여 순차적인 수행 조작을 거치는 합성 단위에 대한 등분할 조작의 방식을 보여주었다.

학생의 비례 추론 과정을 분석하여 발달 모델을 구성하기 위해서는 ‘단위 조정’이 핵심적인 이론적 도구가 될 수 있다고 한 Lee와 Shin (2020)의 결과는 본 연구에 시사하는 바가 크다. 본 연구는 면담 학생들이 가분수가 포함된 분수의 곱셈 과정에서 보여주었던 단위 조정에 의한 양적 조작 방식이 비례 문제를 해결 과정에서 중요한 역할을 하였다고 본다. 구체적으로 하나의 3수준 단위에서 또 다른 3수준 단위 사이의 구조적 전환의 가능성은 ‘재귀 분할의 내재화’와 관련되며, 이는 합성 단위에 대한 스플리팅 조작에 중요한 근거가 될 수 있음을 보였다. 그리고 학생들의 가분수가 포함된 분수 문제 해결 과정에서 나타난 ‘재귀 분할의 내재화’ 여부가 비례 문제 상황을 이해하고, 접근하는 과정에서의 양적 조작 방식과 관련됨을 알 수 있었다.

비례 개념에 대한 문제 해결 과정으로부터 인지 주체인 학생의 추론 방식을 이해하려는 연구들(예, Ahn & Pang, 2008; Carney, et al., 2016; Eom & Kwean, 2011; Hong & Kim, 2013; Ko & Lee, 2007; Park, 2008)은 대부분 학생의 문제 해결 전략과 수준에 주목할 뿐 구체적인 조작 활동에 초점을 두고 학생이 어떠한 방식으로 양들 사이의 관계를 접근해 가는지를 분석한 연구는 드물다. 따라서 본 연구는 같은 단위 조정의 수준에 있는 두 학생을 대상으로 ‘구체적 조작’에 초점을 두어 분수 맥락에서 보여준 단위 조정 방식으로부터 비례 문제 해결 과정을 이해하는데 설명적 도구가 될 수 있음을 확인하였다. 결과를 분석하는 과정에서 두 가지 측면으로의 시사점은 다음과 같다.

첫째, 두 학생이 문제 해결 과정에서 보여준 조작 방식의 차이는 자연수 맥락에서 같은 수준의 단위 조정 단계에 있다 하더라도 분수 맥락에서는 생성되는 단위 구조의 복잡성에 따라 서로 다른 양적 조작 방식으로 구별될 수 있음을 보여주었다. 즉, 분수 맥락에서는 사고 과정이 다를 수 있으므로 단위 조정 이론에 대한 연구의 확장을 시사하는 바이다.

둘째, 분수의 곱셈 상황에서 상연은 수치적 조작에만 의존하며 문제 해결 과정에 양적 조작의 의미가 함께 수반되지 못하였다. 이러한 모습은 비례 문제 상황에서 비례식 알고리즘의 수치적 계산에만 주목했던 초기 면담 과정과도 유사한 모습이다. 이후로 4주 뒤 추가 면담에서 다시 만난 상연은 식의 계산이 안 된다면서 이전에 자신이 사용했던 비례식 알고리즘을 떠올리지 못하였다. 그리고 막대 그림이 주어진 비례 문제를 ‘3분 10초’라는 긴 시간이 걸렸지만, 결국 분할하는 모습을 보여주었다. Thompson (1994)은 양적 조작만으로는 양이 무엇인지 명확히 할 수 없으므로 양적 구조 안에서 구하고자 하는 양을 명확히 하기 위해 수치적 조작도 필요하다고 하였다. 그러나 학생이 형식적 계산에 치중한 수치적 조작만 사용할 경우 복잡한 문제 상황에서 자신이 수행하는 과정에 대한 어떠한 양적 의미도 부여하지 못하게 되어 이후로의 수학 학습에 큰 어려움을 가져올 수 있다(Lee & Lee, 2020; Lee & Shin, 2020; Thompson, 1994). 따라서 양적 구조라는 맥락 안에서 수치적 조작이 학생들에게 의미를 가질 수 있도록 시각적 표상이나 양적 구조로 표상할 수 있는 발문을 포함한 여러 방안을 교수학습 측면에서 모색해 볼 필요가 있다.

한편, 비례 개념이 포함된 닮은 도형에서도 ‘단위 조정’이 중요한 역할을 할 수 있음을 확인하였다. 이후로도 ‘닮은 도형’ 뿐만 아니라 학생들의 분할 조작을 통해 3수준 단위를 조정하는 학생들에 대하여 분수 지식과 다양한 수학적 문제 해결 과정에서의 연구로 확장할 것을 제언한다. 이러한 방향으로의 연구는 초등학교에서의 산술 지식이 중, 고등학교에서 다른 수학 영역으로의 확장되어 실제 학생들이 어떠한 조작 활동으로 무엇을 이해하고 있는지를 설명해 줄 수 있는 기초 연구가 될 것이라고 본다.

Footnote

1 조작은 물리적 행동이 내면화된 정신적 행동이라면, 스킴은 수행되는 활동이라기보다 목표가 수반되는 활동으로 경험 상황, 활동, 결과의 세 가지 요소로 스킴의 목표와 유기적으로 연결되어 서로 영향을 미친다(Steffe & Olive, 2010). 즉, 스킴은 어떤 목표를 달성하고자 조직된 일련의 조작들이다(Hackenberg & Tillema, 2009).

2 Lewin에 의하면 내면화는 상황을 마음속에서 정신적으로 이미지화할 수 있도록 하는 행동의 재구성 과정이라 하였고(as cited in Thompson, 1994), 내재화(interiorization)는 정신적 조작으로서 생각에 따라 수행될 수 있는 점진적인 재구성과 행동의 조직(organization of actions)이라고 보았다(Thompson, 1994). 따라서 본 연구에서는 내면화된 행동이 조작을 위한 구조 안에 구성되면 이를 ‘내재화된 행동’ 또는 ‘조작’이라고 표현할 것이다.

3 Hackenberg와 Tillema (2009)에서 MC1은 활동을 통해 2수준 단위 조정이 가능한 첫 번째 곱셈적 개념이며, MC2는 2수준 단위를 내재화하여 전체에서 부분을 분리하여 전체의 일부로서 구성할 수 있는 2수준 단위의 결과를 조작 가능한 두 번째 곱셈적 개념이다. MC3는 3수준 단위의 내재화로 단위의 모든 수준을 유지하며 연산 과정에서 재귀성을 시사하는 세 번째 곱셈적 개념이다.

4 본 고에서는 $\frac{1}{5}$이 7번 반복된 하나의 단위를 ‘$\frac{1}{5}$의 7-단위’로 표현한다.

5 예를 들면 원래 막대의 $\frac{3}{5}$에 대하여 부분 분수 스킴은 5부분에서 3부분을 빼내는 것으로 이해한다면 반복 분수 스킴은 $\frac{1}{5}$의 3배로 인식하여 곱셈적 관계로부터 분수를 이해하는 것이다. 따라서 반복 분수 스킴을 구성하려면 분할과 반복의 구성인 스플리팅 조작이 필요하다(Steffe & Olive, 2010).

6 합성 단위에 대한 등분할 조작을 구성한 학생도 5로 3을 나누어떨어지게 하기 위해 3을 이루는 각 단일 단위를 어떤 수로 분할하는 활동을 통해 3수준 단위 구조를 구성하는 것이 가능하다(Shin & Lee, 2019). 하지만 3수준 단위 구조를 문제 해결을 위한 주어진 자원으로 사용할 수 없으므로 시행착오를 겪을 가능성이 크다.

7 Johnson은 Thompson의 비 개념에 대한 개념적 분석을 바탕으로 학생의 수준에 따라 ‘동등한 집합으로의 비’, ‘하나당으로의 비’, ‘측정으로의 비’로 구체화하였다. Johnson의 비 개념에 대한 상세한 기술은 Lee와 Lee (2020)를 참고하길 바란다.

8 예를 들면 Lobato 외(2010)는 비례 추론 발달을 위한 선결 조건으로 분수의 의미 즉, $\frac{2}{3}$와 같은 분수를 $\frac{1}{3}$의 2배라는 수학적 의미를 도출하고, 비례 추론의 발달 과정을 하나의 양에서 두 가지 양으로 동시에 인식하는 것으로부터 덧셈 비교에서 곱셈 비교로, 합성 단위 전략에서 곱셈 비교로, 그리고 합성 단위를 반복하는 것에서 무한히 많은 동치인 비를 구성해 내는 것의 변화 과정으로 보았다.

9 현재 중학교 1학년은 자유학년제로 학교에서 수행평가나 지필평가라는 공식적인 평가 방법을 통해 성적을 산출하지 않고, 정성평가로만 평가된다. 따라서 수학 교과 담당 교사의 도움을 받아 ‘2단원 정수와 유리수’를 마친 시점에 수업 시간을 이용하여 한 학급을 대상으로 정수와 유리수에 대한 단원 형성평가(20문제)를 별도로 시행하였다.

10 참여 학생의 이름은 모두 가명임을 밝힌다.

11 ‘complex fraction’은 일반적으로 분수의 분자 혹은 분모 중 적어도 하나가 분수인 ‘번분수’로 Hackenberg와 Tillema (2009)에서는 ‘$\frac{11}{9}$의 $\frac{4}{3}$’와 같이 ‘1보다 큰 가분수’를 포함하여 분수의 곱셈 과제를 ‘complex fraction composition’이라고 표현하였다.

12 자연수 맥락에서 단위 조정 3단계 학생이라면 1-3-33과 1-11-33의 두 개의 구조 사이에서 유연한 조정 즉, 3×11=33과 11×3=33 사이의 변환은 가용 가능한 조작이다.

13 상연은 막대의 분할을 통해 분수 문제를 해결하는 것이 익숙하지 않아서 초반에 눈대중으로 분할했을 수도 있다. 그러나 단위에 단위를 합성하는 문제 상황에서 눈대중으로 분할하는 상연의 모습은 이후로도 자주 등장했던 모습임을 밝힌다.

14 상연은 1에서 인 가분수를 나타냈던 방식과 같이 11부분을 1-단위로 보고 3으로 나누어 를 나타내기 위해 한 번 더 반복하는 조작 활동을 의도했던 것 같으나, 그림에서는 계속 11부분을 4로 나누는 모습을 보였다.

15 상연은 면담 과정에서 지수가 뛴 거리를 세 칸으로 나눈다고 하였으나, 그림으로는 네 칸으로 나누었다. 단위에 단위를 분할해서 나눈 것이 아니므로 12부분이지만 4씩 3개(혹은 3씩 4개)라는 1-4-12(혹은 1-3-12)의 3수준 단위 구조를 구성하지는 못하였음을 보여주는 근거이다.

16 주어진 과제에서는 우유 7컵이었지만 혜지는 이미 우유 4컵은 주어진 양이므로 나머지 우유 3컵에 대한 초코 파우더의 양을 구하기 위해 우유 3컵에 대한 문제 상황으로 인식한 것으로 보인다.

17 면담 당일, 상연은 바로 전 수업이 체육이었다면서 땀을 많이 흘리고 교실에 들어왔다. 체육수업 이후 바로 진행된 면담이라서 그런지 다른 면담 때와는 달리 많이 힘들어 보였고, 중간중간 문제에 집중하지 못하는 모습도 보였다. 상연은 비례식 알고리즘에 의해서 답을 구한 뒤 이어지는 대화에도 다른 시도는 하지 않다. 따라서 면담자는 면담을 마무리하고 4주 뒤에 비슷한 문제 상황으로 다시 면담을 진행하였다.

18 본 고에서는 Hackenberg와 Tillema의 재귀 분할을 ‘일반적인 조작 방식으로 추상화했다’는 의미를 인지 주체가 행위의 결과까지 예측 가능함을 넘어 그 맥락이 아닌 상황에서도 가용 가능한 조작으로 보고, 이를 재귀 분할의 ‘내재화’라고 보았다.